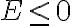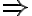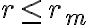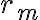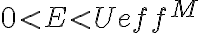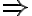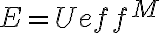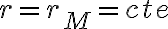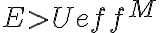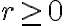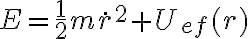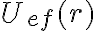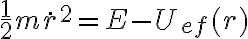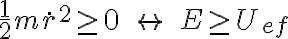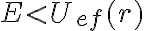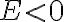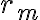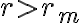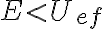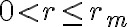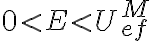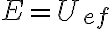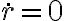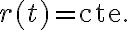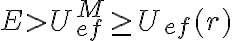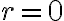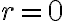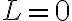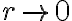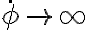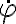Hola, Rodrigo. Buena pregunta y es muy útil hacer este tipo de reflexiones.
Breve repaso: La clave de todo este tema es que para fuerzas centrales es posible demostrar que se mantiene constante
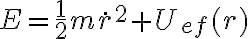
quedando el valor determinado por las condiciones iniciales. Esta ecuación es equivalente a un problema en una dimensión de una partícula que tiene que moverse por un perfil dado por 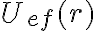 .
.
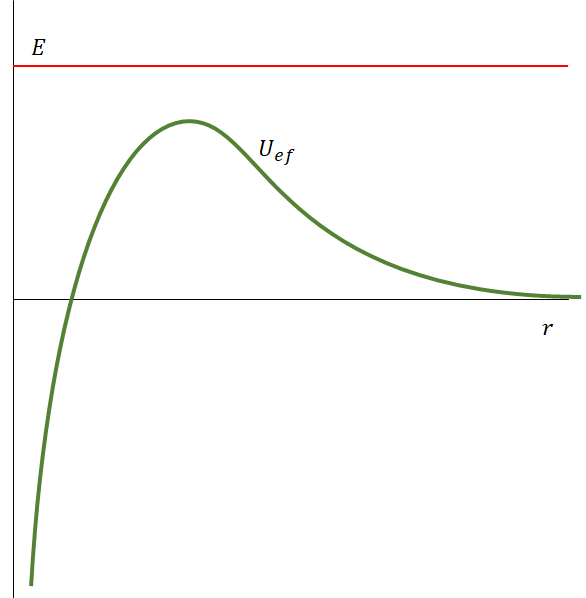
Una forma que me ayuda a entender estas situaciones es pensar en una partícula que se mueve por un terreno que tiene montañas y valles dados por esa función.
De la ecuación anterior se puede despejar el término de «energía cinética»:
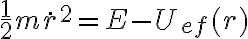
Luego, observamos que, en cualquier parte del movimiento, se debe cumplir
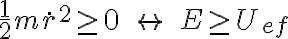
Por lo tanto no es posible observar la partícula en una situación en que 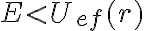 . Esto significa que la partícula tiene el acceso prohibido a cualquier valor de
. Esto significa que la partícula tiene el acceso prohibido a cualquier valor de  donde se cumple esa desigualdad (la partícula no puede «subir la montaña»
si no tiene energía suficiente).
donde se cumple esa desigualdad (la partícula no puede «subir la montaña»
si no tiene energía suficiente).
------
(1) De la gráfica vemos que cuando 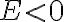 aparece un cierto
aparece un cierto 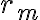 tal que para cualquier
tal que para cualquier 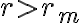 , queda
, queda 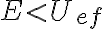 . La conclusión es que, por lo tanto, el movimiento queda restringido a la región
. La conclusión es que, por lo tanto, el movimiento queda restringido a la región 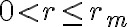 .
.
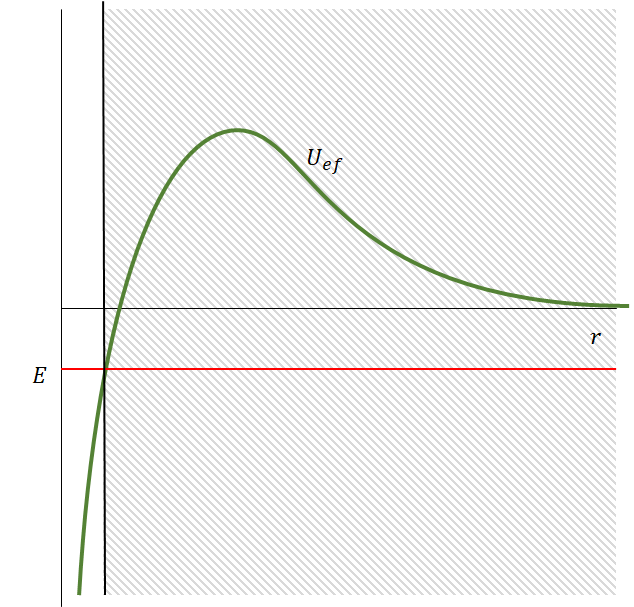
(2) Cuando tenemos 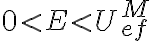 , la región de valores posibles de
, la región de valores posibles de  queda separada en dos intervalos en los cuales puede estar la partícula (uno de ellos va del origen hasta cierto radio y el otro va desde un radio mayor hasta infinito). Dadas las condiciones iniciales que definen en cuál de los intervalos comienza el movimiento, la partícula queda confinada a ese intervalo y no puede pasar al otro.
queda separada en dos intervalos en los cuales puede estar la partícula (uno de ellos va del origen hasta cierto radio y el otro va desde un radio mayor hasta infinito). Dadas las condiciones iniciales que definen en cuál de los intervalos comienza el movimiento, la partícula queda confinada a ese intervalo y no puede pasar al otro.
(3) Si 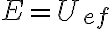 , entonces
, entonces 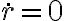 y por lo tanto
y por lo tanto 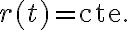 . El radio se mantiene constante, y como también se conserva el momento angular, el movimiento resultante es circular uniforme (en la analogía con el movimiento
1D, la partícula se queda quieta «en la parte más alta de la montaña»).
. El radio se mantiene constante, y como también se conserva el momento angular, el movimiento resultante es circular uniforme (en la analogía con el movimiento
1D, la partícula se queda quieta «en la parte más alta de la montaña»).
(4) Si 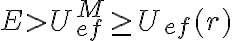 , todos los valores de
, todos los valores de  son accesibles (la energía «alcanza» para recorrer todo el terreno).
son accesibles (la energía «alcanza» para recorrer todo el terreno).
Un último detalle: desde el punto de vista de la energía sería concebible (aunque preocupante) tener 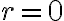 . Pero esto en realidad no puede suceder debido a la conservación del momento angular. ¿Sabrías explicar los detalles?
. Pero esto en realidad no puede suceder debido a la conservación del momento angular. ¿Sabrías explicar los detalles?
Saludos,
NC

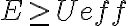 , entonces quería estudiar los diferentes de casos de la energía, pero no logro sacar buenas conclusiones
, entonces quería estudiar los diferentes de casos de la energía, pero no logro sacar buenas conclusiones