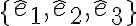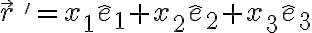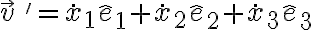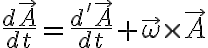Foro de consultas generales

Hola, Mateo. ¿Trataste de resolver los mismos ejercicios por tu cuenta? ¿Llegaste a resultados distintos de los publicados? Ten en cuenta que muchas veces puedes encontrar la respuesta correcta por distintos caminos. En general no es muy eficiente tratar de reproducir idénticamente lo que está en las soluciones y conviene, en cambio, comparar el planteo propio para examinar ventajas y desventajas y posibles errores.

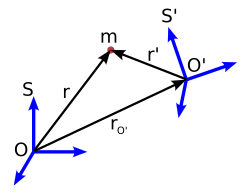
La explicación a tu pregunta proviene de cómo se define la velocidad y la aceleración en términos de las derivadas relativas. Para generalizar, imagina que estás en un sistema de referencia cualquiera con una base formada por vectores fijos con respecto a este sistema:

    $\{\hat e_1, \hat e_2, \hat e_3\}$

e indicamos la posición de un objeto con un vector relativo a ese sistema mediante

    ${\vec r}{\,}' = x_1 \hat e_1 + x_2 \hat e_2 + x_3 \hat e_3$

La derivada relativa se realiza considerando que los vectores de la base correspondiente son fijos. La velocidad relativa a este sistema proviene de derivar el vector de posición:

     ${ \vec v}{\,}' = \dot x_1 \hat e_1 + \dot x_2 \hat e_2 + \dot x_3 \hat e_3$

(y algo análogo para la aceleración relativa). Hasta aquí no hay mucha sorpresa. Incluso si este sistema de referencia aparece rotando respecto a otro con cierta velocidad angular, eso no va a influir en las expresiones de la velocidad y la aceleración. 

En los ejercicios que consultas, al comienzo se determina la velocidad y aceleración relativas a un sistema solidario a la guía o al plano. El movimiento de tal sistema con respecto a otro sistema cualquiera no afecta el resultado, y por lo tanto no aparece la velocidad angular $\omega$ en esta parte.

Luego sí, nos va a interesar tomar en cuenta el movimiento del sistema solidario con respecto a otro sistema de referencia. La velocidad y aceleración en este último se puede ver como el resultado de la composición del movimiento relativo junto con el movimiento del sistema solidario. Para hacer el cálculo, se puede utilizar la relación entre las derivadas con respecto a cada sistema. Para un vector cualquiera se cumple

    $\dfrac {d \vec A}{dt} = \dfrac { d' \vec A}{dt} + \vec \omega \times \vec A$

(la ecuación que relaciona la derivada «absoluta» con la derivada «relativa»). El último término refleja que la rotación de un sistema con respecto al otro puede conducir a un cambio de las coordenadas del vector, aún en el caso en que sea constante en uno de los sistemas.

En las soluciones de los ejercicios que consultaste no se usa directamente este resultado, sino los teoremas de Roberval y de Coriolis, pero es equivalente (los teoremas se demuestran a partir de esta ecuación). Ahí sí se toma en cuenta la velocidad angular de un sistema con respecto al otro.

------

Recomiendo hacer un repaso de la parte de cinemática que estuvimos viendo al principio del curso y rehacer los últimos ejercicios del práctico 1, para convencerse de que se está entendiendo este asunto correctamente.

-----

Saludos,
NC