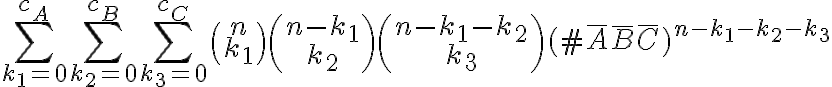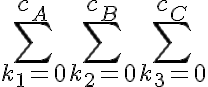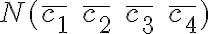Hola, quería consultar sobre un concepto que está relacionado con problemas de combinatoria, del cual tengo algunas dudas. Tal vez esto pueda ir para el parcial, entonces me parece mejor preguntarlo antes.
El problema surge en querer contar la cantidad de palabras de largo  que se pueden formar usando las letras
que se pueden formar usando las letras 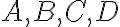 pero que no pueden contener más de
pero que no pueden contener más de 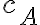 letras
letras  ,
, 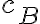 letras
letras  ,
,  letras
letras 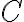 ni
ni 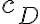 letras
letras 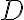 . Para ordenar el problema suponemos que la letra
. Para ordenar el problema suponemos que la letra  es la que aparece en menor cantidad, luego le sigue la
es la que aparece en menor cantidad, luego le sigue la  , luego la
, luego la 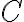 y finalmente la
y finalmente la 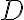 , lo que es equivalente a decir que
, lo que es equivalente a decir que 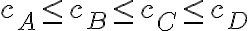 .
.
Comenzando por el caso más fácil, tenemos que  no llega a agotar ninguna letra, por lo que no tenemos restricciones al construir la palabra. Para este caso podríamos plantearnos un problema más sencillo:
no llega a agotar ninguna letra, por lo que no tenemos restricciones al construir la palabra. Para este caso podríamos plantearnos un problema más sencillo:
Contar la cantidad de palabras de largo n que se pueden formar usando las letras 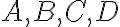 .
.
Debido a que no tenemos limitaciones, la cantidad de palabras posibles sería 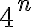 .
.
Luego le sigue el caso donde 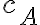 , es decir que nos vemos limitados a usar la letra
, es decir que nos vemos limitados a usar la letra  hasta
hasta 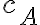 veces. Esto podemos plantearlo como el siguiente problema:
veces. Esto podemos plantearlo como el siguiente problema:
Contar la cantidad de palabras de largo n que se pueden formar usando las letras 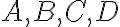 que no contengan más de
que no contengan más de 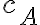 letras
letras  .
.
Este problema podemos resolverlo separando en casos y sumando todas las ocurrencias de las palabras que:
- no contengan la letra
 . Aprovecharemos a utilizar la notación
. Aprovecharemos a utilizar la notación 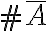 para indicar la cantidad de letras de nuestro conjunto que no son
para indicar la cantidad de letras de nuestro conjunto que no son  , en nuestro caso
, en nuestro caso 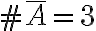 . Luego, la cantidad de palabras que no contienen la letra
. Luego, la cantidad de palabras que no contienen la letra  es
es 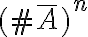 .
. - contengan sólo una letra
 . Esto lo podemos ver como querer agregar una letra
. Esto lo podemos ver como querer agregar una letra  en una palabra de largo
en una palabra de largo  que solo contenga letras
que solo contenga letras  ,
, 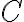 o
o 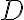 . Si imaginamos
. Si imaginamos  casilleros en donde debemos colocar una letra
casilleros en donde debemos colocar una letra  y el resto llenarlos con las letras de la palabra que no contiene
y el resto llenarlos con las letras de la palabra que no contiene  , podemos decir que tenemos
, podemos decir que tenemos  posibles lugares donde colocar dicha la letra
posibles lugares donde colocar dicha la letra  . Por lo tanto tenemos
. Por lo tanto tenemos 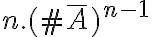 posibles palabras donde la letra
posibles palabras donde la letra  aparecerá sólo una vez.
aparecerá sólo una vez. - contengan sólo dos letras
 . En este caso tendremos que elegir dos lugares entre
. En este caso tendremos que elegir dos lugares entre  disponibles para colocar las letras
disponibles para colocar las letras  ; tendremos
; tendremos 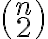 posibilidades para hacerlo. La cantidad de palabras posibles con sólo dos letras
posibilidades para hacerlo. La cantidad de palabras posibles con sólo dos letras  será
será 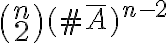
Así vamos repitiendo el cálculo hasta 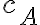 letras
letras  . Entonces la cantidad de palabras que se puedan formar que sólo tengan restricciones en la letra
. Entonces la cantidad de palabras que se puedan formar que sólo tengan restricciones en la letra  es igual a
es igual a 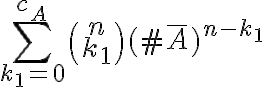 .
.
Continuamos con el problema, y ahora tomamos el caso en el que 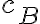 , es decir que
, es decir que  agota dos letras de lo que tenemos permitido usar. El problema ahora toma la siguiente forma:
agota dos letras de lo que tenemos permitido usar. El problema ahora toma la siguiente forma:
Contar la cantidad de palabras de largo n que se pueden formar usando las letras 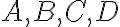 que no contengan más de
que no contengan más de 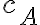 letras
letras  ni tampoco más de
ni tampoco más de 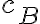 letras
letras  .
.
De nuevo esto lo podemos enfrentar separando por casos, contando las palabras que:
...
...
Como vemos, son demasiados casos, tendríamos que construir una tabla que indique cuantas  y cuantas
y cuantas  tiene que tener cada caso y sumar luego todos los casos.
tiene que tener cada caso y sumar luego todos los casos.
Para el caso donde la palabra no contiene ninguna  pero puede contener
pero puede contener  resulta en
resulta en 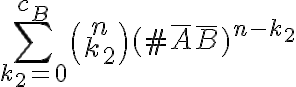 , donde como mencionamos anteriormente
, donde como mencionamos anteriormente 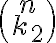 representa las formas de elegir
representa las formas de elegir 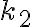 lugares para
lugares para  de
de  disponibles y
disponibles y  representa las formas de armar palabras de largo
representa las formas de armar palabras de largo 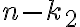 de forma que no tengan ni
de forma que no tengan ni  ni
ni  .
.
Ahora, si agregamos la posibilidad de que la palabra pueda contener  obtenemos
obtenemos 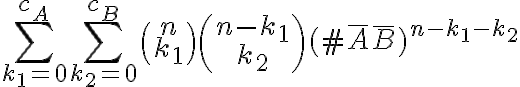 . Notar que los números combinatorios representan las formas de elegir
. Notar que los números combinatorios representan las formas de elegir 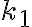 lugares para
lugares para  de
de  disponibles y las formas de elegir
disponibles y las formas de elegir 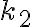 lugares para
lugares para  de
de 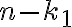 disponibles respectivamente. Como comentario adicional, podemos escribir el resultado también como
disponibles respectivamente. Como comentario adicional, podemos escribir el resultado también como 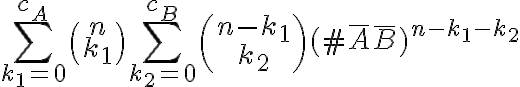 . La idea detrás de esto es algo así como calcular cuantas palabras no tienen ni
. La idea detrás de esto es algo así como calcular cuantas palabras no tienen ni  ni
ni  y luego contar para cada una de ellas de cuantas maneras podemos entremezclar las letras
y luego contar para cada una de ellas de cuantas maneras podemos entremezclar las letras  y
y  .
.
Continuamos y ahora pasamos a la restricción del uso de tres letras, cuando  . El razonamiento es análogo:
. El razonamiento es análogo:
El producto de los números combinatorios es igual al coeficiente multinomial 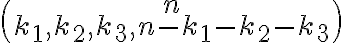 al cual en realidad denotaremos como
al cual en realidad denotaremos como 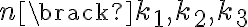 debido a que no nos interesa tener en cuenta el término
debido a que no nos interesa tener en cuenta el término 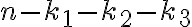 .
.
Notamos que como nuestro conjunto solo tiene cuatro letras, 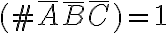 . Entonces nos queda:
. Entonces nos queda:
Ahora, la pregunta es la siguiente. ¿Qué pasa cuando el uso de las cuatro letras está restringido? ¿Pasaríamos a usar  que sería cero? Es decir, ¿de qué manera podemos contemplar este caso aplicando el mismo razonamiento?
que sería cero? Es decir, ¿de qué manera podemos contemplar este caso aplicando el mismo razonamiento?
Agradecería su respuesta.
Saludos.