Buenass, en la parte b de este ejercicio llegué correctamente al resultado de que: G(jω) = P u(jω)P e(jω) y además a cuál son cada una de esas transformadas. Mi tema es que Pu(jw) no depende de k porque w es una frecuencia continua. Entiendo que al hacer el producto con el peine de dirac me queda la función evaluada en los puntos donde se apoya cada delta del peine, o sea kw0. Por eso entiendo que la tansformada sea el sinc evaluado en esos puntos y ta entra a la serie y etc. De todas formas, una vez que llego a esa conclusión para qué sigo necesitando tener la delta en la serie? si ya estoy diciendo que voy a tener la serie del sinc evaluado en kw0. No se si se entiende bien la pregunta.
Hola,
no sé si comprendí tu consulta, pero trataré de responder lo que entendí.
Cuando haces el producto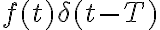
obtenés 
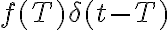, por lo que las deltas aparecen y no podrías eliminarlas.
Adicionalmente, cuando hablamos de series de Fourier, estamos pensando en una secuencia de números (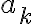
) donde cada uno indica el peso de la frecuencia correspondiente en la señal periódica. El valor del índice 
determina de qué frecuencia estamos hablando.
Cuando hablamos de transformadas de Fourier, estamos pensando en una función continua en la variable
, por lo que debemos indicar claramente en el eje en qué frecuencias tenemos energía (acá el índice no nos auxilia). Cuando las señales temporales son periódicas, nosotros sabemos (gracias a la serie de Fourier) que la energía de la señal está condensada únicamente en las frecuencias múltiplos de la frecuencia fundamental. Naturalmente, cuando vemos la transformada de Fourier de una señal periódica necesitaríamos algún objeto matemático que tenga la capacidad de ser nulo en todo menos en un único valor, y que además su integral (que por Parseval nos indicará la energía) debería ser no nula... por eso necesitamos esas deltas.
Espero haber comprendido tu duda y que esto te pueda ayudar.
saludos
no sé si comprendí tu consulta, pero trataré de responder lo que entendí.
Cuando haces el producto
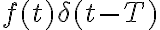obtenés 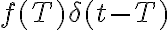, por lo que las deltas aparecen y no podrías eliminarlas.Adicionalmente, cuando hablamos de series de Fourier, estamos pensando en una secuencia de números (
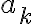) donde cada uno indica el peso de la frecuencia correspondiente en la señal periódica. El valor del índice determina de qué frecuencia estamos hablando.Cuando hablamos de transformadas de Fourier, estamos pensando en una función continua en la variable
, por lo que debemos indicar claramente en el eje en qué frecuencias tenemos energía (acá el índice no nos auxilia). Cuando las señales temporales son periódicas, nosotros sabemos (gracias a la serie de Fourier) que la energía de la señal está condensada únicamente en las frecuencias múltiplos de la frecuencia fundamental. Naturalmente, cuando vemos la transformada de Fourier de una señal periódica necesitaríamos algún objeto matemático que tenga la capacidad de ser nulo en todo menos en un único valor, y que además su integral (que por Parseval nos indicará la energía) debería ser no nula... por eso necesitamos esas deltas.Espero haber comprendido tu duda y que esto te pueda ayudar.
saludos