Buenas, tenia una duda sobre la parte 1b donde pide calcular el 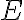 con r>b, como puedo calcularlo?
con r>b, como puedo calcularlo?
En segundo lugar, tenia una duda sobre el 3c tampoco comprendo como calcular el 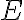 del mismo
del mismo
Gracias
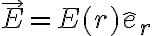 , donde r es la distancia al centro de la esfera cargada y
, donde r es la distancia al centro de la esfera cargada y 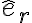 es el versor saliente a la esfera con dirección determinada por el centro de la esfera y el punto de observación (donde queres calcular el campo eléctrico).
es el versor saliente a la esfera con dirección determinada por el centro de la esfera y el punto de observación (donde queres calcular el campo eléctrico). . Asi lo hace la solución. Otra es calcular el campo eléctrico integrando sobre la distribución de cargas. Para la primera hay que tener cuidado que solamente conociendo el campo sobre una parte del espacio (recta, plano, etc) pueda derivarse el campo eléctrico. En este caso, por la simetría del problema se puede hacer. Esto se estudia en la clase 9 de Openfing.
. Asi lo hace la solución. Otra es calcular el campo eléctrico integrando sobre la distribución de cargas. Para la primera hay que tener cuidado que solamente conociendo el campo sobre una parte del espacio (recta, plano, etc) pueda derivarse el campo eléctrico. En este caso, por la simetría del problema se puede hacer. Esto se estudia en la clase 9 de Openfing.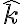 ). Midiendo el ángulo desde esa recta, los extremos de la barra están en ángulos
). Midiendo el ángulo desde esa recta, los extremos de la barra están en ángulos 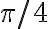 y
y 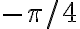 así que esos son tus extremos de integración.
así que esos son tus extremos de integración.