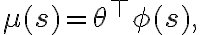Estimados,
comparto una sugerencia para los que quieran usar discretizaciones del espacio de estados para la última parte del entregable.
Podemos pensar en la discretización de la media de la siguiente forma:
donde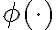 
es un vector de características binario (con ceros y unos). Pueden construirse este vector de características usando Tile Coding (leer Sutton&Barto 2020, sección 9.5.4).
En Tile Coding cada estado se representa con pocos unos y varios ceros. Una de sus ventajas es que estados cercanos tienen representaciones cercanas (es decir, "comparten" unos en posiciones similares). Como consecuencia de esto, al hacer un update de la política (como en REINFORCE, por ejemplo) además de mover la política para el estado particular que consideran, también la están moviendo para estados cercanos.
Hay una implementación muy elegante de Tile Coding hecha por el mismísimo R. Sutton, que usa unas estructuras llamadas Index Hash Tables (IHTs). Pueden leer sobre la implementación acá y bajar el código de python acá. Para correrlo agreguen esta porción de código:
En este caso x e y son la primera y segunda componente del estado y X_MAX y X_MIN los valores límite de la primera componente. La magia está en que la función mytiles() les devuelve los índices del feature vector que tienen un uno en la codificación de Tile Coding.
Cualquier consulta a las órdenes.
Saludos,
Agustin