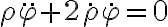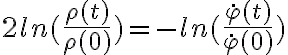Estimada:
El procedimiento número 1 que proponés es correcto. Eso es porque se puede demostrar que en este ejercicio la componente vertical del momento angular es constante. Y esa componente escrita en coordenadas cilíndricas es
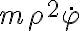 . Luego hay que usar que para que la partícula permanezca en el cono se tiene que verificar que
. Luego hay que usar que para que la partícula permanezca en el cono se tiene que verificar que 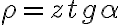 . Observar que a diferencia de los ejercicios de movimiento central, en que se conserva el vector momento angular, en este ejercicio solo se conserva su componente vertical.
. Observar que a diferencia de los ejercicios de movimiento central, en que se conserva el vector momento angular, en este ejercicio solo se conserva su componente vertical. El método de preintegración que allí propone es el siguiente. La componente según 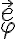 de la aceleración es nula, porque no hay fuerzas en esa dirección. En coordenadas cilíndricas esto es:
de la aceleración es nula, porque no hay fuerzas en esa dirección. En coordenadas cilíndricas esto es:
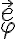 de la aceleración es nula, porque no hay fuerzas en esa dirección. En coordenadas cilíndricas esto es:
de la aceleración es nula, porque no hay fuerzas en esa dirección. En coordenadas cilíndricas esto es: que es lo mismo que:
Integrando respecto al tiempo a ambos lados y haciendo cambios de variables adecuados el término de la izquierda es una integral en 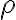 , y el de la derecha una en
, y el de la derecha una en 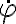 . Haciendo esas integrales da:
. Haciendo esas integrales da:
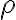 , y el de la derecha una en
, y el de la derecha una en 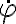 . Haciendo esas integrales da:
. Haciendo esas integrales da: Esto da la misma preintegral de antes, que cambiando a z y evaluando en el instante inicial me lleva a:
Saludos:
Ricardo.