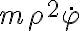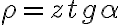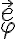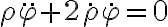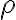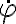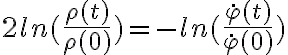MecNew: Ejercicio 11

Hola estuve intentando e intentando llegar a hallar phi punto de dos maneras; 1 suponiendo que m.r^2.phi punto era constante pues su derivada era lo igual a los términos de la segunda ley según del versor en el que no hay aceleraciór; entonces si su derivada es igual a 0 es constante. Pero el phi no me quedó bien; pues lo compré con una repuesta de este mismo ejercicio en el foro y era diferente.

También intente preintegrar el término de la segunda ley según ephi) pero creo que no termine de entender muy bien el procedimiento de preintegracion (lo releí y lo volví a estudiar pero no me queda) pues tampoco me da como la respuesta del foro. Quería saber si podrían enviarme el procedimiento correcto en pasos así entiendo como debería hacerlo; muchas gracias

Re: Ejercicio 11

de Carolina Silveira Recarey - sábado, 24 de abril de 2021, 19:25

Más que nada me interesaría la explicación de cómo resolverlo con la preintegracion, pues se aplica en un montón de ejercicios y la pude hacer en todos, pero en este no

Re: Ejercicio 11

de Ricardo Marotti - domingo, 25 de abril de 2021, 16:29

Estimada:

El procedimiento número 1 que proponés es correcto. Eso es porque se puede demostrar que en este ejercicio la componente vertical del momento angular es constante. Y esa componente escrita en coordenadas cilíndricas es

$m \rho^2 \dot{ \varphi }$ . Luego hay que usar que para que la partícula permanezca en el cono se tiene que verificar que

$\rho = z tg \alpha$ . Observar que a diferencia de los ejercicios de movimiento central, en que se conserva el vector momento angular, en este ejercicio solo se conserva su componente vertical.

El método de preintegración que allí propone es el siguiente. La componente según

$\vec{e}_\varphi$ de la aceleración es nula, porque no hay fuerzas en esa dirección. En coordenadas cilíndricas esto es:

$\rho \ddot{ \varphi } + 2 \dot{ \rho } \dot{ \varphi } = 0$

que es lo mismo que:

$2 \frac{ \dot{ \rho } }{ \rho } = - \frac{ \ddot{ \varphi } }{ \dot{ \varphi } }$

Integrando respecto al tiempo a ambos lados y haciendo cambios de variables adecuados el término de la izquierda es una integral en

$\rho$ , y el de la derecha una en

$\dot{ \varphi }$ . Haciendo esas integrales da:

$2 ln( \frac{ \rho(t) }{ \rho(0)} ) = - ln( \frac{ \dot{ \varphi } (t)}{ \dot{ \varphi }(0) } )$

Esto da la misma preintegral de antes, que cambiando a z y evaluando en el instante inicial me lleva a:

$\dot{ \varphi } = \frac{H v_0}{tg \alpha z^2}$

Saludos:

Ricardo.