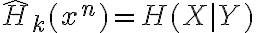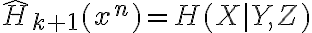Buenas, estoy trancado con este ejercicio.
Lo primero que habia intentado para probar que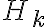 
es decreciente fue tratar de establecer alguna recurrencia o algun conjunto de transformaciones que me permitieran usar induccion, pero no se me ocurrio nada. Lo segundo fue tratar de llevar la expresion de 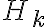a una expresion que solo dependa de k (y de la tira 
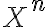), o sea escribirla en funcion de k, encontrando expresiones para 
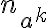y demas numeros definidos en funcion de k, pero tampoco logre nada.
Por donde podria arrancar?
Saludos,
Rafael
