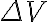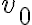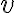Hola, subo una foto de lo que hice para este ejercicio ya que no encuentro mi error y el resultado que obtengo es distinto al de las soluciones. Saludos!
Hola, lo que pasa es que el 
varía con la velocidad, de modo que el equilibrio que planteaste se cumpla en todo momento. Entonces en lugar de 
va 
en la expresión para y eso te cambia la ecuación difefencial.
Saludos!
varía con la velocidad, de modo que el equilibrio que planteaste se cumpla en todo momento. Entonces en lugar de va en la expresión para y eso te cambia la ecuación difefencial.Saludos!
Hola Anaclara!
No entiendo qué cambia el hecho de que la integral tenga a v en lugar de vo. De dónde sale el log(2)?
Hay alguna forma de escribir v en función del largo de la barra? porque, si no me equivoco, ese es el diferencial de la ecuación, no?
Hola, no entiendo bien porqué ΔV varía con la velocidad, si me lo podes explicar te agradezco. Saludos!
Buenas,
Juan Arrospide Orsi:
Luego de obtener la intensidad en función de la velocidad (que va a ir decayendo) vas a usar la segunda ley de Newton para obtener una ecuación diferencial en la velocidad. Debido a que la velocidad varía, uno no puede fijarla. El logaritmo de dos aparece naturalmente cuando resuelvas la ecuación diferencial.
Facundo Campal Caputti:
La variación de potencial se produce por la diferencia de cargas que se generan en la barra. Las positivas bajan, la negativas suben. Esta diferencia genera un campo eléctrico. Recordar la ecuación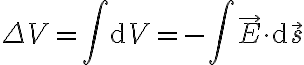
. El campo eléctrico, a su vez, está en equilibrio con la fuerza magnética. Como esta última depende de la velocidad vemos que por transitiva el potencial depende de la velocidad.
Juan Arrospide Orsi:
Luego de obtener la intensidad en función de la velocidad (que va a ir decayendo) vas a usar la segunda ley de Newton para obtener una ecuación diferencial en la velocidad. Debido a que la velocidad varía, uno no puede fijarla. El logaritmo de dos aparece naturalmente cuando resuelvas la ecuación diferencial.
Facundo Campal Caputti:
La variación de potencial se produce por la diferencia de cargas que se generan en la barra. Las positivas bajan, la negativas suben. Esta diferencia genera un campo eléctrico. Recordar la ecuación
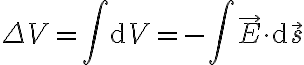. El campo eléctrico, a su vez, está en equilibrio con la fuerza magnética. Como esta última depende de la velocidad vemos que por transitiva el potencial depende de la velocidad.Saludos