Hola, buenos días.
Al intentar resolver la parte a) llego a una integral complicada que no se resolver y sospecho debo tener algún error, no se si en las cuentas o en como plantee la integral inicialmente.
Para calcular el V(P) provocado por la varilla, considero que la varilla esta formada por varios dq en todo su largo desde 0 a L.
"Y" es la distancia de P al punto mas cercando a la varilla, y es cte, "r" es la distancia de P a cada punto "x" de la varilla, que es variable, a "r" la expresé como sqrt(x^2+y^2) por Pitágoras.
La distribución de carga por unidad de longitud es lambda que a su vez vale kx, así que dq lo expresé como dq=k(x^2)
La integral me quedo V(P)=integral desde 0 a L de la función k(x^2)/4*pi*epsilon0* sqrt(x^2+y^2) diferencial x.
Con el cambio de variable u=sqrt(x^2+y^2) du=x/ sqrt(x^2+y^2) me queda la integral siguiente:
V(P)= integral desde Y hasta sqrt(L^2+y^2) de la función (k/4*pi*epsilon)* sqrt(u^2-y^2) diferencial u.
Y en este punto quede trancado
Agradezco la ayuda!
Hola,
el problema ahí es que escribiste mal el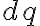
. Un diferencial de carga en la barra se puede escribir como la densidad lineal por un diferencial de longitud, es decir 
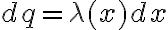(lo podés pensar como que estás calculando la carga de un pedacito de barra). Así que la integral te queda 
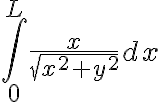. Fijate si con eso te sale.
Saludos!
el problema ahí es que escribiste mal el
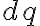. Un diferencial de carga en la barra se puede escribir como la densidad lineal por un diferencial de longitud, es decir 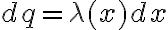(lo podés pensar como que estás calculando la carga de un pedacito de barra). Así que la integral te queda 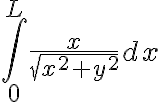. Fijate si con eso te sale.Saludos!
Muchas gracias, quedó claro!