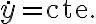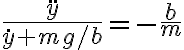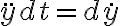Hola, Bruno. Tu pregunta es muy relevante y muy importante.
* Sucede que el espacio de ecuaciones diferenciales posibles es tan grande que, desafortunadamente, no hay un método universal que se pueda aplicar indiscriminadamente para todos los casos.
* Por otra parte, vale la pena tomar en cuenta que las derivadas de algunas funciones tienen cierta "persistencia", como por ejemplo las exponenciales, las polinómicas y las trigonométricas. Al derivar estas funciones obtenemos una nueva función de aspecto similar, y por lo tanto podemos tener ciertas expectativas de que nos permitan determinar una solución particular de la ecuación diferencial. En este caso habría que ensayar diferentes opciones hasta dar con una que sirva.
Para este proceso también ayuda tomar en cuenta que estas ecuaciones describen un sistema mecánico, de manera que hay ciertas opciones que se pueden considerar o no en base al comportamiento esperado del sistema. Por ejemplo, una función seno o coseno podrían ser (eventualmente) soluciones de un sistema oscilatorio, pero no del movimiento de un proyectil.
* La buena noticia es que hay un subconjunto de ecuaciones diferenciales en las que sí es posible desarrollar técnicas universales para obtener una solución particular: las ecuaciones diferenciales lineales. En este caso es posible aplicar el método del polinomio característico para resolver el problema, al transformarlo en un problema algebraico y ayuda a sistematizar la búsqueda.
* Finalmente: para la situación específica del ejercicio del práctico, conviene empezar ensayando las funciones más simples posibles, es decir,
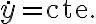
, a ver qué tal...
En realidad, la ecuación diferencial a la que se llega es lineal no homogénea, pero además es de variables separables. Eso significa que se puede manipular para llevarla a una forma que se puede integrar directamente. Si quieres hacer el intento, trata de llegar a
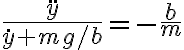
¿Es posible plantear una integral a partir de ahí? (pista:
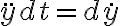
) ¿Cuáles son los límites de integración correspondientes? ¿El resultado coincide con la solución encontrada por el otro método?
Espero haber podido ayuidar. Contanos cómo te va y consulta si hay más dudas.
Saludos,
NC