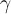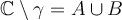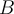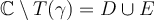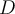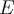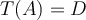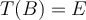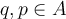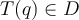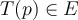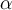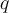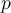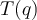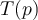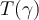Practico 2

Practico 2

de Santiago Federico Avila Pujadas -
Número de respuestas: 7

Disculpen, la semana pasada no pude asistir a clase y vi que subieron videos resolviendo la parte a del ejercicio 1, un compañero dio el ejercicio 6 y otro el ejercicio 8. Me estoy perdiendo de algo o fue esto nomas lo que dieron en practico?

Porque me complique con el ejercicio 4 y no logro entender como seria la transformacion un conjunto

En respuesta a Santiago Federico Avila Pujadas

Re: Practico 2

de Favio Piran -
Hola. Sí, esos fueron los ejercicios que trabajamos. También mencioné algunas cosas relacionadas al ejercicio 1 que sirven para el 5 por ejemplo.
De transformación de conjuntos hablamos en el ejercicio 8, esto no es más que la imagen de un conjunto por una función (en este caso una transformación de Möbius).
Para el ejercicio que mencionás, una transf de Möbius manda una cfa o recta en una cfa o recta. Tanto una cfa como una recta dividen al plano complejo en dos componentes conexas, por lo tanto hay que ver qué componente conexa va en cuál otra (si tenemos la transf de Möbius explícita no es más que evaluar en algún punto para averiguar cuál). Concretamente en ese ejercicio que manda una cfa en cfa, hay que ver si el interior de la cfa se manda por T en el interior de la cfa imagen o la manda "afuera". Eso es la parte a).

Si no podés avisá. De todas formas yo voy a entrar un rato antes a la clase y me quedo un rato después para evacuar dudas.
Te recuerdo también que hay un grupo de telegram para entre todos ayudar a destrancar los ejercicios.

Saludos!
En respuesta a Favio Piran

Re: Practico 2

de Denis Gabriel Peña Presa -
Una pregunta Favio, el hecho de que una tranformación de Möbius te lleve una componente conexa en una compenente conexa viene dado porque las tranformaciones de Möbius son invertibles ¿No? Porque cualquier recta que conecte dos puntos pertenecientes a la misma componente conexa, no se te puede cortar con el borde (que divide diferentes componentes) luego de pasado por la tranformación, porque las transformaciones de Möbius son continuas en C /(-d/c) ¿o me equivoco?
En respuesta a Denis Gabriel Peña Presa

Re: Practico 2

de Favio Piran -
Exactamente. Las transformaciones de Möbius son continuas en el plano complejo extendido, ya que está bien definida la continuidad en el infinito. Más aún las transformaciones de Möbius son homeomorfismos (función continua e invertible con inversa continua) del plano extendido en sí mismo.
Luego lo que se usa es que es biyectiva y que la imagen de un conjunto conexo por una función continua tiene que ser conexo. Pero en este caso se puede probar como decís, usando curvas:

Si \gamma es la recta o cfa y T es la transformación de Möbius, \mathbb{C} \setminus \gamma = A\cup B donde A y B son las componentes conexas. Por otro lado \mathbb{C} \setminus T(\gamma) = D \cup E donde D y E son componentes conexas. Hay que ver que T(A)=D y T(B)=E o al revés.
Para ver esto alcanza con ver, por la biyectividad de T, que no pueden existir dos puntos en A que vayan a parar a diferentes componentes conexas. Es decir, no existen q,p \in A tales que T(q)\in D y T(p)\in E (o al revés).
Suponiendo (razonando por absurdo) que sí existen tales puntos, tomando una curva \alpha en A que una los puntos q y p se puede probar (con un argumento tipo Bolzano) que la imagen de la curva \alpha (que es una curva que une T(q) con T(p)) necesariamente tiene que cortar a la curva T(\gamma), lo que es un absurdo ya que T(\gamma) no está en la imagen de A.
En respuesta a Favio Piran

Re: Practico 2

de Denis Gabriel Peña Presa -
Buenísimo, gracias por responder Favio. Una consulta más ¿Algún libro que recomiendes para profundizar en estos temas? Topología de Munkres ¿Puede ser?
En respuesta a Denis Gabriel Peña Presa

Re: Practico 2

de Favio Piran -
Si. Podés leer el capítulo 3 del Munkres que es sobre conexión.
Si estás interesado en estos temas en Facultad de Ciencias tenés un curso sobre introducción a la topología, donde básicamente se tratan los temas de la primer parte de ese libro.
Saludos!
En respuesta a Favio Piran

Re: Practico 2, Ej.4

de Javier Martin Perez Tejeira -
Buenas noches. Estoy intentando hacer los repartidos y en el segundo no estoy viendo cómo resolver la primer parte del ejercicio 4. En el mismo se da la Transformación con su expresión. Y de determina un conjunto D que es la parte de adentro del círculo unidad.
Y pide probar que T(D)= D, puede ser que sea simplemente un montos de operaciones? Igual no veo como "acomodar" esas operaciones para llegar a probarlo.
Saludos y gracias