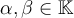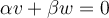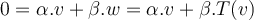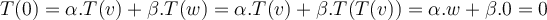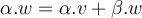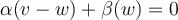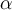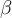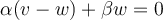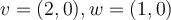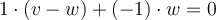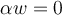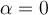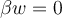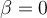Buenas noches,
No estoy seguro si es correcto preguntar sobre estos ejercicios o no, pido disculpas si no corresponde.
Una de las preguntas que me toco es la siguiente y sinceramente no logro ver el porque de la respuesta correcta:
"Sea  un espacio vectorial de dimensión 2 y
un espacio vectorial de dimensión 2 y 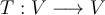 un operador lineal tal que
un operador lineal tal que 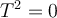 , pero
, pero 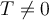 .
.
Sea 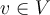 tal que
tal que 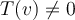 . Si
. Si 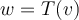 . Entonces el conjunto es una base de
. Entonces el conjunto es una base de  . ¿Verdadero o falso?"
. ¿Verdadero o falso?"
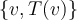 es base de
es base de 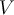 , y se puede afirmar que
, y se puede afirmar que 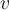 y
y 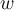 son distintos entre si, porque
son distintos entre si, porque 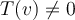 y
y 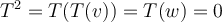 .
.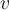 y
y 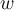 sean linealmente independientes, para de esta manera poder concluir si forman una base o no.
sean linealmente independientes, para de esta manera poder concluir si forman una base o no.