Buenas , queria saber si me puede dar alguna ayuda para resolver estos dos ejercicios que no me salieron , muchas gracias.
Hola, a continuacion te cuento como podias resolver esos ejercicios.
Para el primero, como todo subconjunto no vacio de
no vacio de  debe tener un minimo, dados dos elementos cualesquiera
debe tener un minimo, dados dos elementos cualesquiera 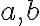 de
de  estos deben estar relacionados por
estos deben estar relacionados por  , o sea
, o sea 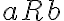 o bien
o bien 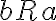 pues si no estuvieran relacionados podrias considerar el conjunto
pues si no estuvieran relacionados podrias considerar el conjunto 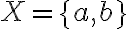 y este
y este  no tendria minimo (recuerda que un elemento es minimo de un conjunto debe estar en el conjunto, y estar relacionado con todos los elementos del conjunto, o sea
no tendria minimo (recuerda que un elemento es minimo de un conjunto debe estar en el conjunto, y estar relacionado con todos los elementos del conjunto, o sea  es minimo de
es minimo de  si
si 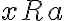 para todo
para todo  en
en  y ademas
y ademas 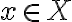 ). Entonces todos los elementos de
). Entonces todos los elementos de  deben estar relacionados entre si, por lo tanto
deben estar relacionados entre si, por lo tanto  debe ser un orden total. Basta entonces contar ordenes totales en
debe ser un orden total. Basta entonces contar ordenes totales en  . Como
. Como  tiene
tiene  elementos hay
elementos hay 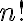 ordenes totales en
ordenes totales en  . La respuesta correcta es la e.
. La respuesta correcta es la e.
Para el segundo ejercicio, se puede resolver con funciones generatrices como lo vimos en el curso o tambien asi:
como de la primera ecuacion sabes que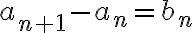 entonces de aqui deducis que
entonces de aqui deducis que 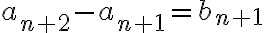 .
.
Entonces tenes a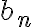 y a
y a 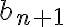 en funcion de los terminos de la sucesion
en funcion de los terminos de la sucesion  , asi que sustituyendo
, asi que sustituyendo 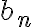 y a
y a 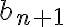 en la segunda ecuacion, obtenes una ecuacion solo en funcion de los terminos de la sucesion
en la segunda ecuacion, obtenes una ecuacion solo en funcion de los terminos de la sucesion  que te queda homogenea de segundo orden:
que te queda homogenea de segundo orden: 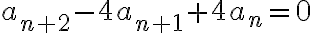 . Resolviendo la homogenea te queda
. Resolviendo la homogenea te queda  pues 2 es raiz doble en el polinomio caracteristico. Hallas las constantes
pues 2 es raiz doble en el polinomio caracteristico. Hallas las constantes 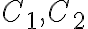 con las condiciones iniciales:
con las condiciones iniciales: 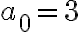 y
y 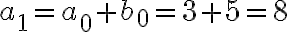 y asi te queda
y asi te queda 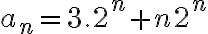 , entonces
, entonces 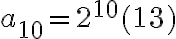 .
.
Ademas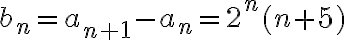 asi que
asi que 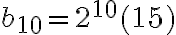 . La respuesta correcta es la d.
. La respuesta correcta es la d.
Para el primero, como todo subconjunto
 no vacio de
no vacio de  debe tener un minimo, dados dos elementos cualesquiera
debe tener un minimo, dados dos elementos cualesquiera 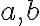 de
de  estos deben estar relacionados por
estos deben estar relacionados por  , o sea
, o sea 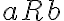 o bien
o bien 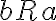 pues si no estuvieran relacionados podrias considerar el conjunto
pues si no estuvieran relacionados podrias considerar el conjunto 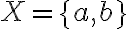 y este
y este  no tendria minimo (recuerda que un elemento es minimo de un conjunto debe estar en el conjunto, y estar relacionado con todos los elementos del conjunto, o sea
no tendria minimo (recuerda que un elemento es minimo de un conjunto debe estar en el conjunto, y estar relacionado con todos los elementos del conjunto, o sea  es minimo de
es minimo de  si
si 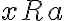 para todo
para todo  en
en  y ademas
y ademas 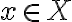 ). Entonces todos los elementos de
). Entonces todos los elementos de  deben estar relacionados entre si, por lo tanto
deben estar relacionados entre si, por lo tanto  debe ser un orden total. Basta entonces contar ordenes totales en
debe ser un orden total. Basta entonces contar ordenes totales en  . Como
. Como  tiene
tiene  elementos hay
elementos hay 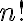 ordenes totales en
ordenes totales en  . La respuesta correcta es la e.
. La respuesta correcta es la e.Para el segundo ejercicio, se puede resolver con funciones generatrices como lo vimos en el curso o tambien asi:
como de la primera ecuacion sabes que
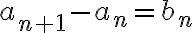 entonces de aqui deducis que
entonces de aqui deducis que 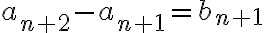 .
.Entonces tenes a
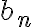 y a
y a 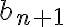 en funcion de los terminos de la sucesion
en funcion de los terminos de la sucesion  , asi que sustituyendo
, asi que sustituyendo 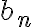 y a
y a 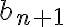 en la segunda ecuacion, obtenes una ecuacion solo en funcion de los terminos de la sucesion
en la segunda ecuacion, obtenes una ecuacion solo en funcion de los terminos de la sucesion  que te queda homogenea de segundo orden:
que te queda homogenea de segundo orden: 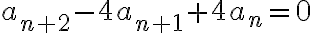 . Resolviendo la homogenea te queda
. Resolviendo la homogenea te queda  pues 2 es raiz doble en el polinomio caracteristico. Hallas las constantes
pues 2 es raiz doble en el polinomio caracteristico. Hallas las constantes 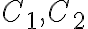 con las condiciones iniciales:
con las condiciones iniciales: 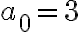 y
y 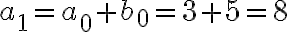 y asi te queda
y asi te queda 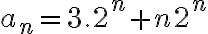 , entonces
, entonces 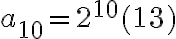 .
. Ademas
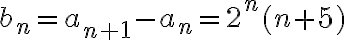 asi que
asi que 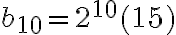 . La respuesta correcta es la d.
. La respuesta correcta es la d.Excelente , Muchas gracias !!
