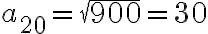Buenas, me podrían explicar como hacer este ejercicio? No pude llegar a la respuesta correcta.

Buenas, me podrían explicar como hacer este ejercicio? No pude llegar a la respuesta correcta.

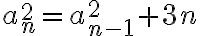 o equivalentemente
o equivalentemente 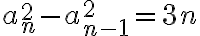 . Fijate que si haces cambio de variable
. Fijate que si haces cambio de variable 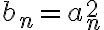 la ecuacion te queda
la ecuacion te queda 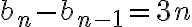 que es lineal de primer orden no homogenea, con condicion inicial
que es lineal de primer orden no homogenea, con condicion inicial 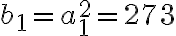
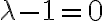 cuya raiz es 1. Por lo tanto, la solucion de la homogenea queda
cuya raiz es 1. Por lo tanto, la solucion de la homogenea queda 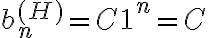 siendo C una constante.
siendo C una constante. 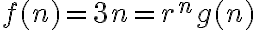 con
con 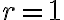 y
y 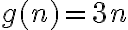 la solucion particular
la solucion particular 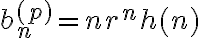 (pues r=1 es justo raiz del polinomio caracteristico, ver notas del curso), siendo
(pues r=1 es justo raiz del polinomio caracteristico, ver notas del curso), siendo  un polinomio del mismo grado que
un polinomio del mismo grado que 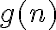 . Entonces
. Entonces 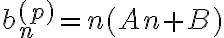 . Sustituyendo en la ecuacion
. Sustituyendo en la ecuacion 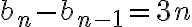 obtenes que
obtenes que 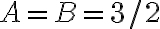 por lo tanto
por lo tanto 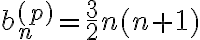 .
. 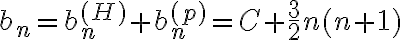 . Imponiendo la condicion inicial
. Imponiendo la condicion inicial 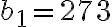 llegas a que
llegas a que 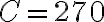 . Luego
. Luego 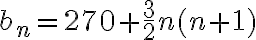 y como
y como 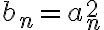 entonces
entonces  . Sustituyendo
. Sustituyendo 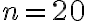 llegas a
llegas a