Buenas, consulto por el ejercicio que dice x1 + x2 + x3 = 21 con -3 <= xi <= 10 como restricción.
Me di cuenta que no hay opción de formar 21 si al menos un xi es negativo por lo que seria igual que decir 1 <= xi <= 10 por así decirlo.
Igual no tengo claro como podría resolverlo si esto no se cumpliera (Ej: x1 + x2 + x3 = 21 con -3 <= xi <= 15 ). Supongo que usando un cambio de variable, pero no se como afecta el que haya que hacer 3 cambios y eso.
Espero que me halla hecho entender.
Gracias

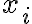
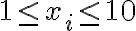
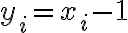
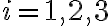
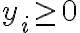
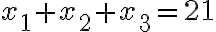
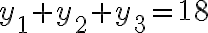
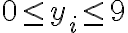
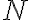
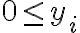
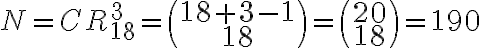
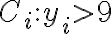
![N(\bar{C_1}\bar{C_2}\bar{C_3})=N-[N(C_1)+N(C_2)+N(C_3)]+[N(C_1C_2)+N(C_1C_3)+N(C_2C_3)]-N(C_1C_2C_3) N(\bar{C_1}\bar{C_2}\bar{C_3})=N-[N(C_1)+N(C_2)+N(C_3)]+[N(C_1C_2)+N(C_1C_3)+N(C_2C_3)]-N(C_1C_2C_3)](https://eva.fing.edu.uy/filter/tex/pix.php/3a3ad4c960bc89b3c257a2d9cc0b5eb5.gif)
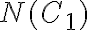
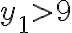
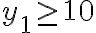
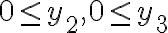
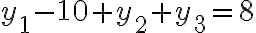
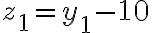
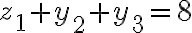
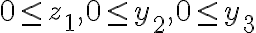
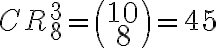
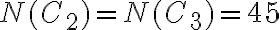
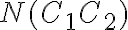
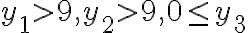
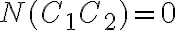
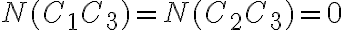
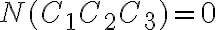
![N(\bar{C_1}\bar{C_2}\bar{C_3})=N-[N(C_1)+N(C_2)+N(C_3)]=190-[45+45+45]=55 N(\bar{C_1}\bar{C_2}\bar{C_3})=N-[N(C_1)+N(C_2)+N(C_3)]=190-[45+45+45]=55](https://eva.fing.edu.uy/filter/tex/pix.php/1fb392127b3aae59dd60a895cf6458d3.gif)