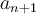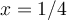Lourdes, hago comentarios sobre la solución.

La idea de la misma es utilizar la recurrencia que define a 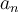 para encontrar una ecuación que verifique
para encontrar una ecuación que verifique 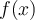 , su función generatriz. Luego con la ecuación obtenida, se despeja el valor
, su función generatriz. Luego con la ecuación obtenida, se despeja el valor 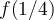 .
.
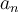 para encontrar una ecuación que verifique
para encontrar una ecuación que verifique 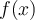 , su función generatriz. Luego con la ecuación obtenida, se despeja el valor
, su función generatriz. Luego con la ecuación obtenida, se despeja el valor 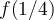 .
.En la segunda linea: se parte de la igualdad de la primer linea. Primero se sustituye la expresión de la izq por 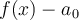 . En la expresión de la derecha, se toma el
. En la expresión de la derecha, se toma el 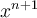 y se lo separa en 3 factores:
y se lo separa en 3 factores:  que sale para afuera de la sumatoria,
que sale para afuera de la sumatoria, 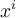 que queda multiplicando a
que queda multiplicando a 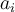 (recordar que buscamos una fórmula para
(recordar que buscamos una fórmula para 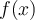 ) y
) y 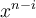 que queda multiplicando a
que queda multiplicando a 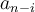 . Si observás, la expresión que resulta no es más que la convolución de
. Si observás, la expresión que resulta no es más que la convolución de 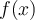 consigo misma, multiplicada por
consigo misma, multiplicada por  . Por eso el resultado es
. Por eso el resultado es 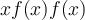 .
.
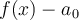 . En la expresión de la derecha, se toma el
. En la expresión de la derecha, se toma el 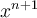 y se lo separa en 3 factores:
y se lo separa en 3 factores:  que sale para afuera de la sumatoria,
que sale para afuera de la sumatoria, 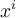 que queda multiplicando a
que queda multiplicando a 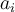 (recordar que buscamos una fórmula para
(recordar que buscamos una fórmula para 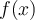 ) y
) y 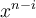 que queda multiplicando a
que queda multiplicando a 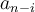 . Si observás, la expresión que resulta no es más que la convolución de
. Si observás, la expresión que resulta no es más que la convolución de 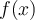 consigo misma, multiplicada por
consigo misma, multiplicada por  . Por eso el resultado es
. Por eso el resultado es 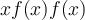 .
.Si te queda alguna duda vuelve a preguntar.
Saludos