Buenas,
No logro entender como hacer este ejercicio. Me pueden dar una guía?
Gracias!
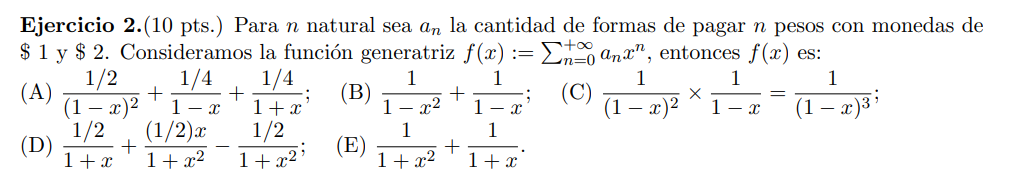
Buenas,
No logro entender como hacer este ejercicio. Me pueden dar una guía?
Gracias!
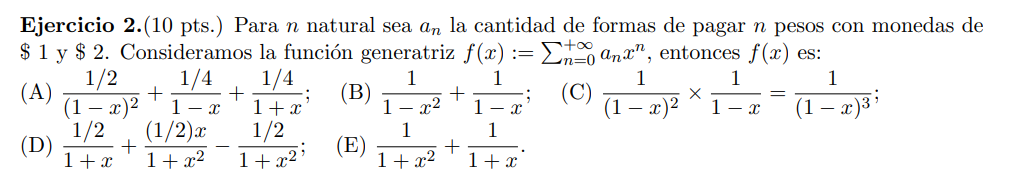
Hola Lourdes
La función generatriz que cuenta la cantidad de formas de pagar  pesos se obtiene como
pesos se obtiene como 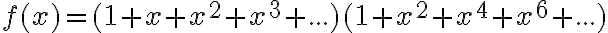 donde el primer factor corresponde a las contribuciones posibles en monedas de $1 y el segundo a las contribuciones posibles en monedas de $2.
donde el primer factor corresponde a las contribuciones posibles en monedas de $1 y el segundo a las contribuciones posibles en monedas de $2.
Por lo tanto 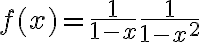 . Lo que resta a partir de aquí es reescribir la expresión como suma de fracciones simples. Haciendo esa cuenta llegás a que la respuesta correcta es la A.
. Lo que resta a partir de aquí es reescribir la expresión como suma de fracciones simples. Haciendo esa cuenta llegás a que la respuesta correcta es la A.
Saludos