Buenas, no entendí que pide calcular el ejercicio, y la solución no me ayudo a darme cuenta.
Podrían explicarme?
Gracias!
EJERCICIO 1 - PRIMER PARCIAL 2DO SEMESTRE 2020
Número de respuestas: 6
En respuesta a Lourdes Alejandra Couto Burgos
Re: EJERCICIO 1 - PRIMER PARCIAL 2DO SEMESTRE 2020
de Claudio Qureshi -
Hola Lourdes. ¿Te referís al ejercicio del embarajado? (es que habían varias versiones por eso pregunto)
En respuesta a Claudio Qureshi
Re: EJERCICIO 1 - PRIMER PARCIAL 2DO SEMESTRE 2020
Ese mismo, te adjunto la letra 
En respuesta a Lourdes Alejandra Couto Burgos
Re: EJERCICIO 1 - PRIMER PARCIAL 2DO SEMESTRE 2020
de Claudio Qureshi -
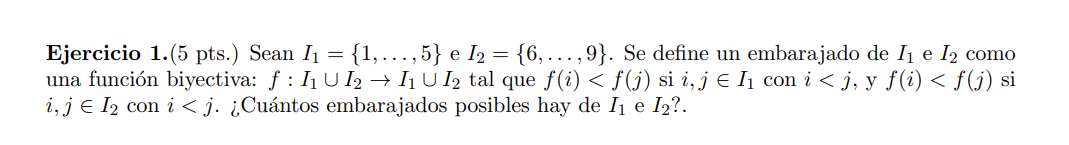
El ejercicio pide calcular el número de funciones biyectivas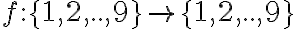 
tales que:
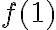y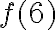 
(a esas funciones se la llaman embarajados).
La observación principal es que para determinar el embarajado basta con conocer quien es el conjunto imagen de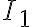 
, o sea, conocer quien es 
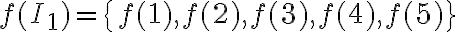. Por ejemplo, si sabemos que 
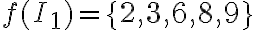(tiene cardinal 5 porque f es inyectiva) entonces necesariamente 
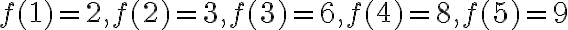. Además como f es biyectiva tenemos 
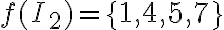por lo tanto 
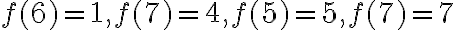. Luego la función 
queda determinada (pues conocemos las imagenes de todos los elementos del dominio).
La otra observación es que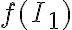 
puede ser cualquier subconjunto de tamaño 5 de 
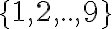. Que tenemos 
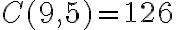posibilidades.
Espero que haya quedado más clara la respuesta de la solución.
Hay otra forma también quizás un poco más visual que es la siguiente. Tenés 9 lugares _ _ _ _ _ _ _ _ _ donde en cada lugar tenés que colocar un número del 1 al 9, entonces para formar un embarajamiento podés hacerlo asi: seleccionás 5 lugares cualesquiera para colocar los números del 1 al 5, por ejemplo: _ _ _ _ _ _ _ _ _ (seleccionamos los lugares 2,3,5,6 y 8). Entonces como tienen que ir ordenados tenés _ 1 2 _ 3 4 _ 5 _ y luego los números del 6 al 9 tienen que ir ordenados en los huecos que sobran asi que nos queda 6 1 2 7 3 4 8 5 9 (que corresponde a la función f tal que f(1)=6, f(2)=1, f(3)= 2, etc). Entonces lo único que tuvimos que hacer fué seleccionar los 5 lugares entre los nueve posible y para eso hay 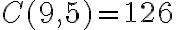posibilidades.
En respuesta a Claudio Qureshi
Re: EJERCICIO 1 - PRIMER PARCIAL 2DO SEMESTRE 2020
Muchas gracias por la respuesta,
Pero me quedo una duda, ¿porqué las C(9,5) garantizan que se cumple la condición de orden entre cada f(i) < f(j) para i,j pertenecientes a I1?
En respuesta a Lourdes Alejandra Couto Burgos
Re: EJERCICIO 1 - PRIMER PARCIAL 2DO SEMESTRE 2020
de Claudio Qureshi -
Eso es porque independientemente de cualquiera de los C(9,5) subconjuntos que te tomes, que llamamos A={a1,a2,a3,a4,a5} (que sin perder generalidad podemos suponer a1<a2<a3<a4<a5) podés armarte un embarajamiento f:{1,2,..,9} --> {1,2,..9} que verifique f(I1)=A siguiendo el siguiente procedimiento:
1. Definis primero f(1)=a1, f(2)=a2, f(3)=a3, f(4)=a4 y f(5)=a5 (eso porque ya habíamos supuesto que tomábamos los elementos de A de forma ordenada, sino habría un paso previo que sería ordenar primero todos los elementos de A). Esto garantiza que f(I1)=A.
Ahora llamemos B={b1,b2,b3,b4} al complemento de A (o sea, aquellos números enteros entre 1 y 9 que no están en A), que nuevamente sin pérdida de generalidad podemos suponer que están ordenados b1<b2<b3<b4.
Como queremos que la f sea una biyección entonces necesariamente f(I2)=B y como queremos que sea un embarajamiento entonces necesariamente debes definir f(6)=b1, f(7)=b2, f(8)=b3 y f(9)=b4.
¿Qué herramientas o técnicas vistas durante el curso estamos usando para resolver este ejercicio?
Lo que usamos fué un "argumento combinatorio" (del estilo del ejercicio 6 del práctico 3) que consiste en que si querés contar cuantos elementos tiene un conjunto B entonces basta con encontrar un conjunto A que sea fácil de contar y probar que existe una biyección F: A -->B. Entonces concluis que #B= #A. Te digo esto porque si preguntás tanto supongo que no te preocupa tanto solo entender este ejercicio sino que te interesa entender bien como se resuelve cualquier ejercicio de este tipo en general.
En este caso particular el conjunto B que nos interesa contar su cardinal es el conjunto de los embarajamientos f:{1,..,9}--> {1,..,9} que se definian como las funciones tales que sus restricciones a I1 es creciente y la restricción a I2 es creciente. El conjunto A que es fácil de contar es el de subconjuntos de {1,..,9} de tamaño 5, cuyo cardinal es C(9,5). La biyección F:A --> B viene dada por el algoritmo que dije arriba (que verifica F(A)=f implica f(I1)=A).
(fijate que usé la notación para los conjuntos A y B en negrita para que no te confundas con los conjuntos A y B del comienzo)
La función F es sobreyectiva: Dada cualquier embarajamiento f en B, si A=f(I1) (que es un elemento de A) es claro que F(A)=f.
(formalmente esto prueba que el cardinal de A es mayor o igual que el cardinal de B)
La función F es inyectiva: Si F(A1)=F(A2)=f entonces f(I1)=A1 y f(I2)=A2, luego A1=A2.
(formalmente esto prueba que el cardinal de B es mayor o igual que el cardinal de A).
Luego #B= #A= C(9,5).
----
Espero que te ayude. El análisis del argumento combinatorio es talvez más dificil de entender que la solución de este ejercicio particular pero la ventaja es que si lo entendés te puede ayudar a resolver cualquier ejercicio de este tipo en general.
En respuesta a Claudio Qureshi
Re: EJERCICIO 1 - PRIMER PARCIAL 2DO SEMESTRE 2020
Muchas gracias!!