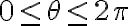 ,
, ![0\leq\rho\leq\sqrt [2] { z } 0\leq\rho\leq\sqrt [2] { z }](https://eva.fing.edu.uy/filter/tex/pix.php/672c0ea7efd7463c2e25c6d645a75178.gif) ,
,  pero no estoy pudiendo encontrar hasta que valor llega
pero no estoy pudiendo encontrar hasta que valor llega  , me pueden ayudar con esto? muchas gracias
, me pueden ayudar con esto? muchas gracias
Hola,
La geometría del problema no se presta mucho para las coordenadas que elegiste. Por ejemplo, no es cierto que el radio 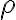 deba variar entre
deba variar entre  y un cierto valor en función de
y un cierto valor en función de  sin tener en cuenta
sin tener en cuenta  .
.
Yo creo que lo mejor es observar que lo que tenes es un paraboloide cortado con un plano. El corte va a quedar una elipse en el espacio dada por las ecuaciones
Si elimino la variable  lo que estoy obteniendo es la proyección ortogonal en el plano
lo que estoy obteniendo es la proyección ortogonal en el plano 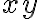 de esta elipse, cuya ecuación es
de esta elipse, cuya ecuación es
 , lo cual es una circunferencia que no esta centrada
, lo cual es una circunferencia que no esta centrada 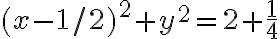
entonces el ejercicio lo que esta pidiendo es calcular el volumen que queda comprendido por la gráfica de dos funciones ( y
y 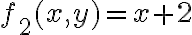 definidas sobre un dominio
definidas sobre un dominio 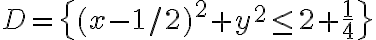
entonces teniendo en cuenta la función que hay que integrar y la forma del dominio, lo más conveniente parece ser hacer polares centradas en 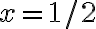 e
e 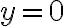 . Con eso la función a integrar
. Con eso la función a integrar 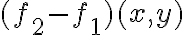 queda simple, y el dominio también, pues
queda simple, y el dominio también, pues 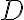 es un circulo.
es un circulo.
Por cierto, en este caso plantear la cuenta como la integral doble de la diferencia entre las funciones es lo mismo que calcular la integral triple de la función 1 sobre la región determinada por las gráficas. Pensado como integral triple las coordenadas serían cilíndricas centradas en el punto 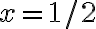 e
e 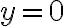 y la variable
y la variable  va entre
va entre 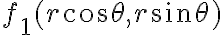 y
y 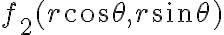 .
.
Te dejo las cuentas para terminar! Decime si me explique bien sino seguimos discutiendo
Saludos
Quedo clarísimo todo, Muchas gracias!