Buen día,
Estoy queriendo probar el lemma pedido en la parte 5.5
Lemma e55 : forall (m : Memoria) (e : BoolExpr) (v : Valor), beval m e = v <-> BEval m e v.
Comencé la prueba por los distintos lados del iff, en ambos casos haciendo induccion sobre e y en ambos casos me tranco al momento de probar el paso inductivo de e = ~ e.
probando: beval m e = v -> BEval m e v.
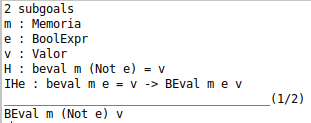
probando: BEval m e v -> beval m e = v.
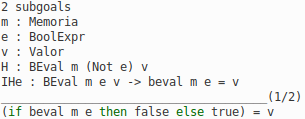
Alguna idea de como continuar la prueba?
Mi idea es que tengo mal definidio o bien BEval o beval ya que la prueba no parece ser posible con esas hipotesis, adjunto las definiciones de las mismas pero al ser respuestas de practico entiendo si esto es editado luego
BEval not:
match e with
...
| enott : forall (e : BoolExpr), BEval m e true ->
BEval m (Not e) false
| enotf : forall (e : BoolExpr), BEval m e false ->
BEval m (Not e) true.
end.beval (m : Memoria) (e: BoolExpr) : Valor :=
match e with
...
| Not e1 => match (beval m e1) with
true => false
| false => true
end
end.Gracias!
