Holi, me puse hacer unos ejercicios de teórico y quería ver si estaba bien, o si tengo ideas erróneas, que probablemente haya, estos los saqué de un parcial viejo, era un v o f, peo aquí van mis razonamientos para ver si acerté
El primero dice, Si A ⊂ R10 es un conjunto generador de R10 , entonces existe un subconjunto A ⊂ A que es una base de R10. Este me pareció verdadero, porque si A es un generador, entonces pueden quitársele algunos vectores para hacerlo LI, por ello un subconjunto que puede ser de hasta R10 o más chico.
La segunda es, Sea T : R9 → M3×3 una transformación lineal. Si existen una base A de R9 y una base B de M3×3 tales que B(T )A = O9 , entonces T (v) = O3 para todo v ∈ R9. Este creo que sí es verdadero, porque significa que la base B en la base A vale O, o sea que todo v, sea el valor que tenga, al ser T(v) va a dar O, ésto es porque es la matriz nula la base B.
La tercera dice, Sean V un espacio vectorial y W1 , W2 dos subespacios vectoriales de V. Entonces el conjunto W = W1 ∪ W2 es un subespacio vectorial de V. Falso, porque no se asegura que la unión de subespacios sea un subespacio.
La cuarta es, Sea T : V → W una transformación lineal inyectiva entre dos espacios vectoriales V y W de dimensión n. Entonces para toda base B = {v1 , ...vn } de V , el conjunto {T (v1 ), ..., T (vn)} es una base de W. En esta tengo bastante duda, pero pareciérame que es verdadera, no encontré ningún contraejemplo pero tampoco siento que pueda probarla, capaz se me hace que puede ser falsa y que sólo se de en caso que sea biyectiva, por la idea que en, por ejemplo, un fog de funciones, un fog biyectivo es una relación uno a uno, éso sí puede ser
La quinta dice, El conjunto W = {A ∈ M3×3 : A no es invertible} es un subespacio vectorial de M3×3, aquí encontré de ejemplo a la matriz nula así que podría ser verdadero, porque además el M3x3 para ser generador de subespacio debe contener a la matriz nula
El sexto, Sean A una base de R5 , B una base de M2×2 y C una base de R3 [X]. Entonces para todas
transformaciones lineales T : R5 → M2×2 y S : M2×2 → R3 [X], tenemos que C (S ◦ T )A =
C (S)B × B (T )A . Sí, esta es una propiedad, es verdadera.
También tengo una duda, si en un ejercicio de este nuevo parcial, me preguntan algo estilo "Sean los puntos O = (1, 1, 1), P1 = (0, 8, 6) y P2 = (8, 2, 6). Se escriben π al plano que pasa por los tres puntos O, P1 y P2 , r a la recta que pasa por los dos puntos P1 y P2 , y d a la distancia entre la recta r y el punto O. Sean π1 y π2 los dos planos a distancia d del plano π. Entonces las ecuaciones de π1 y de π2 son..." hay una manera de resolverlo usando lo que aprendimos recientemente no? Porque intenté hacer justamente éste, y me da la impresión que sí o si va a haber algo de geometría en el parcial, pero me cuesta vincular a la geometría con lo que dimos ahora, sino no sé bien del todo cómo hacerlo
Y luego la última con la que me quedó duda es, si teniendo v1 = (1, 1, 1, 1), v2 = (1, −1, 0, 1), v3 = (1, 2, 3, 4), v4 = (2, 3, 4, 5) y v5 = (3, −1, 3, 7), en ese caso {v1 , v2 , v3 } es LI, v4 y v5 ∈ [{v1 , v2 , v3 }], no? estos de acá a veces me cuestan pero es sólo hacer la matriz e ir descartando hasta que quede LI, yo ahí descarté v5 y v4, y luego hice matriz y descubrí que v1,v2,v3 pueden llegar a dar a v5 y v4, así que me dio éso
Luego, estas dos;
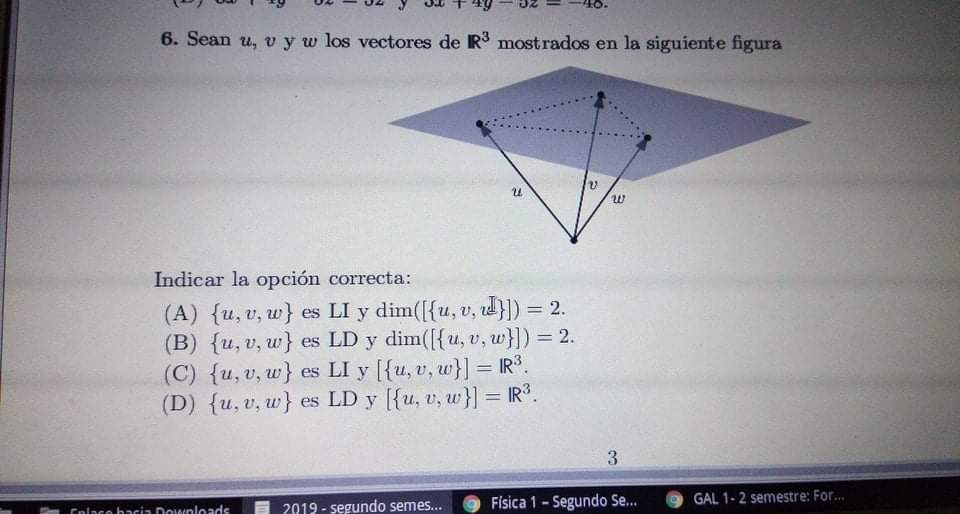

en la primera me dio que es la C, están en R3, puesto que allí se puede ver que parten de algún punto del eje z, y tienen direcciones diferentes, por tanto son LI, no hay ninguna que siga la misma dirección que otra, así lo pensé, y en la segunda, la dimensión de S1 es 2, contiene dos vectores, el (1, 0) y (1, 1), y si yo hago la suma de S1 con S2, me da los vectores (2, 1) y (2, 2), y ellos no son múltiplos de (1, 1) y (-1, 1), así que la b, creo
que te parece?
no sé si es el foro correcto para plantear ésto, de todas formas voy a intentar elegir parciales con las respuestas escritas así no atomizo tanto
