Buenas, no logro comprender por qué la primer afirmación es falsa. Mi razonamiento fue, si converge absolutamente entonces converge, y si la integral converge la función debe tender a 0 en infinito para que el área quede determinada. Traté de buscar algún contraejemplo para poder negar la afirmación pero no se me ocurrió ninguno.
Hola Nicolás. Para construir un contraejemplo pensá en una función no negativa, que valga cero casi siempre pero en el entorno de cada entero se forma un "chichón" de altura 1, cada vez más angosto de modo que el área bajo la curva sea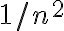 
. Así la integral es como la serie de 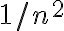y la función cumple todas lás hipótesis de I.