Foro Práctico 6

Hola Bruno, tenés razón. Fue un desliz en el video que corregiremos pronto.

En efecto 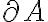$\partial A$ no tiene por qué estar incluido en 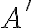$A'$. Y en consecuencia no es cierto que $A' = \partial A \cup int(A)$.

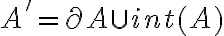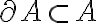Lo que sí se puede decir, es una de las inclusiones: Tomando como hipótesis cualquiera de los otros dos enunciados (que $A$ es cerrado o que $\partial A \subset A$), se puede ver que $A' \subset \partial A \cup int(A) = A$.

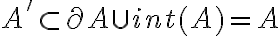En palabras, esto quiere decir que los puntos de acumulación sí o sí tienen que ser, o bien interiores al conjunto (caso en el cual todos los puntos son de acumulación), o bien en la frontera, en la cual no todos los puntos son de acumulación (como bien dijiste) pero lo importante es que no puede haber puntos de acumulación que no estén en uno u otro ya que serían exteriores a $A$ y no podríamos acercarnos a ellos por puntos de $A$.

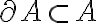Luego como por hipótesis $A$ es cerrado (o bien $\partial A \subset A$, dependiendo de cual tomes por hipótesis), tenemos que 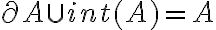$\partial A \cup int(A) = A$ y termina la demostración.