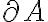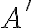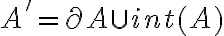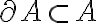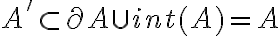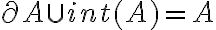Buenas, en el video resolución del ej: 6)c, cuando prueba el segundo sii usa que int(A) está incluido en A´ y que frontera(A) está incluido en A´, entonces A´=int(A) U front(A).
Lo que no me queda claro es por qué la frontera(A) está incluida en A´.
Porque si hay puntos aislados esos serían frontera pero no de acumulación entonces la frontera no estaría incluida en A´, no?
Gracias
Hola Bruno, tenés razón. Fue un desliz en el video que corregiremos pronto.
En efecto 
no tiene por qué estar incluido en 
. Y en consecuencia no es cierto que 
.
Lo que sí se puede decir, es una de las inclusiones: Tomando como hipótesis cualquiera de los otros dos enunciados (que 
es cerrado o que 
), se puede ver que 
.
En palabras, esto quiere decir que los puntos de acumulación sí o sí tienen que ser, o bien interiores al conjunto (caso en el cual todos los puntos son de acumulación), o bien en la frontera, en la cual no todos los puntos son de acumulación (como bien dijiste) pero lo importante es que no puede haber puntos de acumulación que no estén en uno u otro ya que serían exteriores a y no podríamos acercarnos a ellos por puntos de .
Luego como por hipótesis es cerrado (o bien , dependiendo de cual tomes por hipótesis), tenemos que 
y termina la demostración.