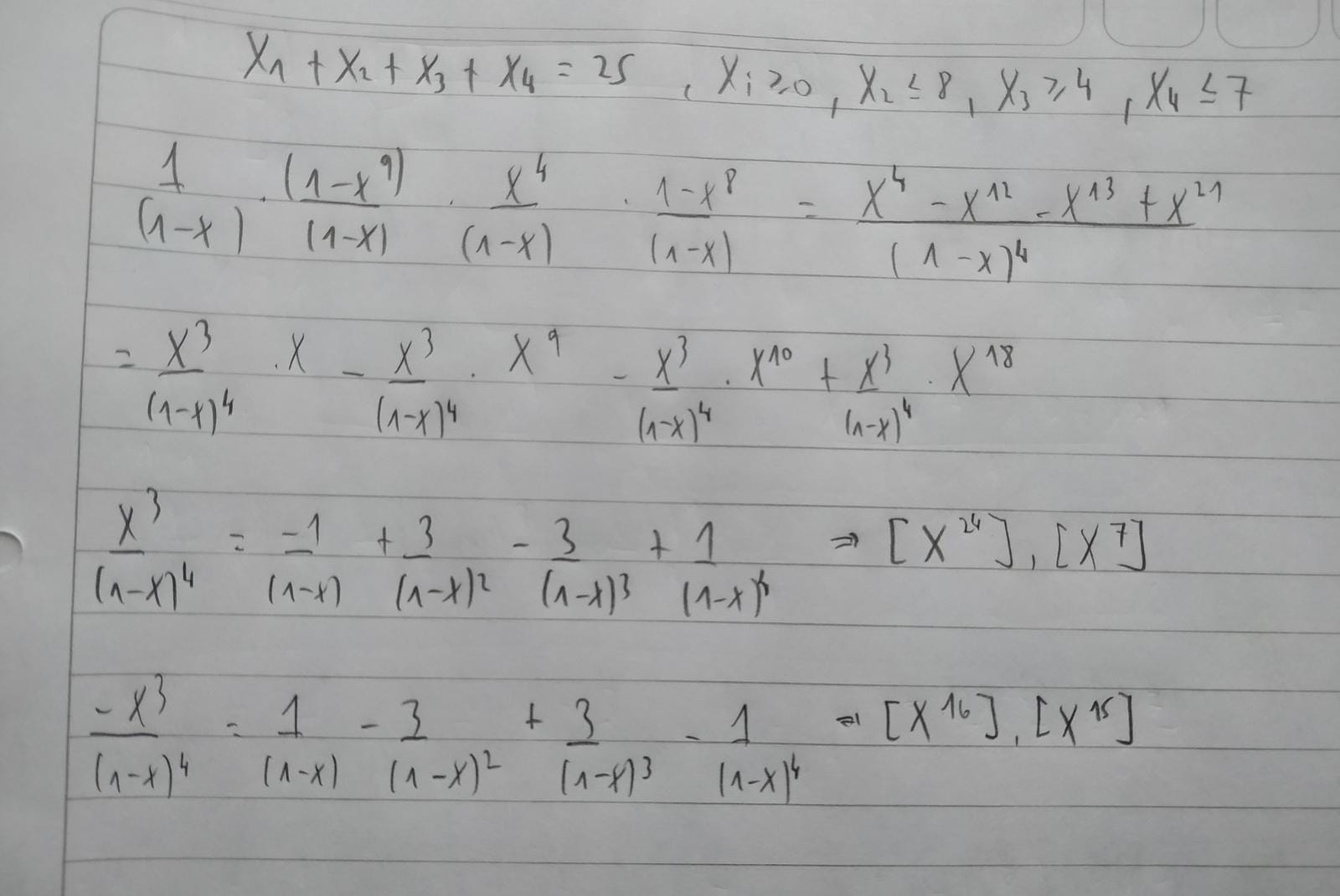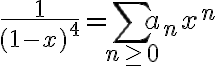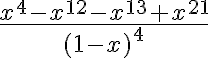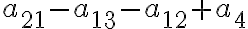Hola tuve dificultades con estos dos ejercicios. En el 1 intente plantearlo como una fila de 50 elementos y luego por casos. En estos, segun el a1 que seleccionaba de las tres opciones, veia que posibilidades tenia para el elemento 50, dependiendo si el a49, era igual que el a1 o no. Tambien intente analizar si se sumaban casos, si el a2 y a48 eran iguales pero no pude llegar a la solucion.
El 2 es parecido al 7 del parctico 5 pero no me da la respuesta, adjunto el planteo por si estan mal las funciones.
Por ultimo repasando me surgio una duda de un ejercicio del practico 4, y la planteo aca por si aquel foro ya no se revisa. Es del ejercicio 13b, en el que llegue a la respuesta pero analizandolo nuevamente nose si la forma en que lo resolvi es correcta, o si se adecuaria a mas casos. Como tenian que ser divisibles por 3, plantee como c1, c2, c3 ser multiplo de 5, 7 y 11 resp. El tema es que eso lo hice para los 1155 numeros "continuos". Una vez que halle la cantidad de numeros que no cumplian esas condiciones, lo dividi entre tres para llegar a la solucion, porque en cada terna de los que no cumplen, solo hay 1 que me interesa quitar, por ejemplo:
5, 10 y 15, quito los tres pero deberia solo el 15, en : 7, 14 , 21, solo deberia el 21, y en : 11, 22, 33 solo el 33, etc.
El tema es que supongo que la eleccion de condiciones fue agrede para que notacemos esto? o si me piden condiciones con numeros no tan "familiarizados" podria proceder de esta manera y dividir al final o como tendria que hacer.
Porque tambien creo que vi que algunos dividieron de una 1155 entre 3 y trabajaron a partir de eso, pero segun lo que entendi del Grimaldi, el principio de inclusion-exclusion, funciona para cantidades continuas, y no tiene forma de saber que al dividir entre 3, estamos quitando el 4, 5, etc. Es asi o estoy equivocado?
Desde ya gracias, saludos,
Rodrigo.