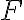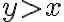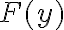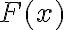Hola, intente realizar el ejercicio 1 y no se por donde arancar, estaria bien negar a lo que queremos llegar para hacerlo por absurdo?
Y el ejercicio 2 parte d, es la integral de la derivada de arctan(t) , pero sus etremos son - y + infinto, lo que hice fue separar en dos integrales y calcularlos por separado, na de - infinito a 0 y la otra de 0 a + infinito, y luego ver si convergen o no, y las dos convergen a pi/2. estaria correcto?
Muchas gracia y saludos
Diego : )
Hola Diego, con respecto al ejercicio 1: muchas veces es una buena estrategia intentar probar algo por absurdo, sobre todo si no tenés mucha idea de por dónde empezar. En el caso de este ejercicio tengo la impresión de que pensar por absurdo puede ayudarte a entender por qué los resultados son ciertos, pero a la hora de escribir puede ser más fácil buscar una prueba directa.
Como sugerencias, para la primera parte fijate que: Para ver que 
es creciente tendrías que tomar 
y ver que pasa con 
y 
. Te sugiero ver cómo se relacionan estos últimos 2, usando la definicion de .
Para las siguientes partes, puede ser útil tener en cuenta que
.
Y para la parte b), los resultados de la parte a) te van a servir.
Fijate si eso te sirve para empezar y si no lo seguimos discutiendo.
Con respecto al ejercicio 2, está bien la estrategia que proponés (notar que la función que estás integrando es siempre positiva). Y fijate que en ese argumento se usa la propiedad que mencionaba más arriba (la integral impropia como límite de la primitiva).
Saludos