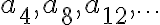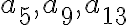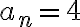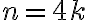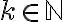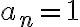Buenas
En este ejercicio se me ocurrió definir una sucesión an tal que a1 = 1, a2 = 2, a3 = 3, a4 = 4, a5 =1, a6 =2, a7 =3 ... y así sucesivamente, de forma que existen subsucesiones convergentes en 1, 2, 3 y 4 y por ende 1, 2, 3 y 4 puntos de acumulación. Mi inconveniente es cómo definir la sucesión an. Porque se podría hacer de forma informal como hice arriba. ¿Cómo puedo definir an?¿Por recurrencia? De ser por recurrencia me darían una mano con eso.
Muchas gracias.
Hola Santiago, una forma posible de definir tu sucesión es aprovechando la periodicidad de la misma.
¿Cómo se interpreta esto en términos de los índices? Fijate que, por ejemplo, tu sucesión vale 4 en los términos 
. Es decir en todos los que tienen índice múltiplo de 4. Mientras que la sucesión vale 1 para los términos 
, que también incrementan sus índices de 4 en 4, pero "desfasados". Algo similar ocurre con los demás términos de la sucesión.
Entonces, por ejemplo, podés decir que tu sucesión cumple que 
si 
, con 
. Ahí tendrías una parte de la definición (tu sucesión quedó definida para todos los índices múltiplos de 4).
Tomando esto como punto de partida ¿te das cuenta de cómo podrías escribir los casos que faltan? ¿Qué tiene que pasar para que, por ejemplo, 
?
Perfecto. Había supuesto eso pero no sabía si era la forma apropiada de definir dicha sucesión.
Muchas gracias