Hola! En el ejercicio 3.1.b por ejemplo el punto a) me queda de la siguiente forma:
S((5,y)t) = (y,5)t está bien?
Lo que no sé como encarar es el punto c, de demostrar la biyectividad y su inversa. Alguna orientación? Gracias!
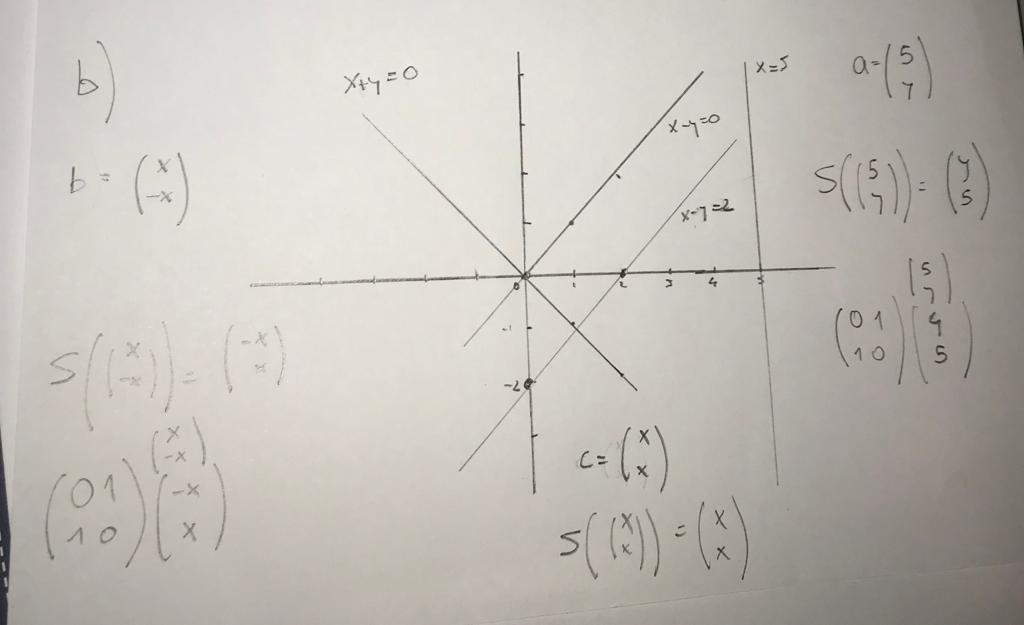
Hola! En el ejercicio 3.1.b por ejemplo el punto a) me queda de la siguiente forma:
S((5,y)t) = (y,5)t está bien?
Lo que no sé como encarar es el punto c, de demostrar la biyectividad y su inversa. Alguna orientación? Gracias!

Hola Enrique,
Es correcto. Veo que en tu dibujo solamente representaste las rectas originales, estaría bueno que también grafiques las rectas obtenidas una vez aplicada la función. Continuando con tu ejemplo, esto sería representar la recta $$y=5$$.
Te recuerdo que una función es biyectiva si es inyectiva y sobreyectiva, Para que S sea sobreyectiva se debe cumplir que $$\forall(a,b)\in\mathbb{R}^2$$ $$\exists$$ $$(x_0,y_0)\in\mathbb{R}^2$$ tal que $$S(x_0,y_0)=(a,b)$$, mientras que para que sea inyectiva se debe cumplir que $$\forall (a,b),(c,d)\in\mathbb{R}^2$$ si se cumple que $$S(a,b)=S(c,d)$$ entonces se verifica que $$(a,b)=(c,d)$$. También se puede demostrar directamente la biyectividad de una función si se prueba que $$\forall(a,b)\in\mathbb{R}^2$$ $$\exists!$$ $$(x_0,y_0)\in\mathbb{R}^2$$ tal que $$S(x_0,y_0)=(a,b)$$ donde el símbolo $$\exists!$$ significa que existe y además es único.
Luego para la parte de la inversa te recuerdo que la función inversa $$S^{-1}$$ cumple que dados dos vectores $$X$$, $$Y$$ de $$\mathbb{R}^2$$ se verifica que $$S(X)=Y\Longleftrightarrow{} S^{-1}(Y)=(X)$$. Fijate si a partir de esa definición lográs darte cuenta cómo sería la inversa de S.
Si no quedó claro algo no dudes en volver a preguntar.
Saludos