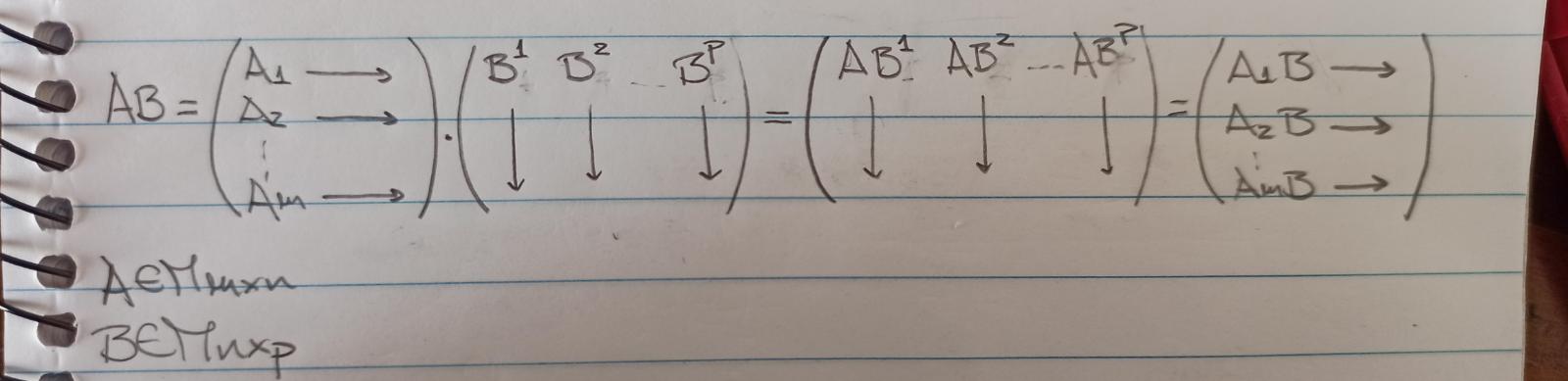GAL1-2S: Ejercicio 1.5.a

Buenas tardes, estoy viendo que esta afirmación es verdadera pero no encuentro un buen modo de justificarla.

La redacción de mi justificación sería:

"Verdadero, puesto que si tomo matrices \( A \) y \( B \) con la particularidad de que en \( B \), \( (b_{11}, b_{21}, ..., b_{m1}) = (b_{13}, b_{23}, ..., b_{m3}) \) O sea que las columnas 1 y 3 son iguales.

Si realizo el producto \( AB \) la sumatoria de todos los productos de la matriz \( A \) por la columna 1 de \( B \) será la misma que la sumatoria de todos los productos de la matriz \( A \) por la columna 3 de \( B \) puesto que son las mismas columnas en \( B \) y las operaciones realizadas son las mismas la columna 1 y 3 de \( AB \) son iguales."

No estoy muy seguro de si está bien la justificación y no se como darme cuanta que hice mal así que cualquier comentario ayuda.

Gracias

Re: Ejercicio 1.5.a

de Bruno Dominguez - viernes, 4 de septiembre de 2020, 16:18

Hola Daniel, estas en lo correcto. Sin embargo, cuando decís "la sumatoria de todos los productos de la matriz A por la..." está expresado un poco raro, supongo que lo que quisiste poner es que el producto de la matriz A por la columna 1 de B es igual al producto de A por la columna 3 de B.

Esto es correcto xq al hacer el producto entre dos matrices este lo podes pensar, por como está definido, como si cada columna j de \(AB\) es igual a \(AB^j\) o como si cada fila i de \(AB\) es igual a \(A_iB\), siendo \(B^j\) la columna j de B y \(A_i\) la fila i de A.

Re: Ejercicio 1.5.a

de Daniel Edgardo Pellejero Morales - viernes, 4 de septiembre de 2020, 16:57

Muchas gracias profe, tenía esa duda.

Esa redacción es mucho más sencilla, pasa que quise describir toda la operación que se hace en una columna cuando se hace el producto de matrices, pero si se puede simplificar así mejor porque queda menos cargado.

Gracias y Saludos