Estimados,
En la clase de hoy se dio una interesante discusión con el siguiente diagrama de bloques (¡sencillísimo!) cuando alguien preguntó: ¿qué pasa si K no es constante?
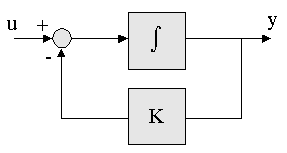
Teníamos escrito algo así:
sin mucho cuidado con la variable de integración y asumiendo 
. De donde, derivando, obtuvimos la ecuación diferencial que nos pedía el ejercicio:
. De donde, derivando, obtuvimos la ecuación diferencial que nos pedía el ejercicio:
Cuando sugirieron la posibilidad de hacer K dependiente del tiempo, me confundí por no prestar atención a la variable de integración y al significado del diagrama de bloques.
El diagrama de bloques, interpretado de una forma natural en el tiempo (y asumiendo que ), debe entenderse así:
), debe entenderse así:
ya que la salida del bloque K(t) se interpreta, en este caso, como la multiplicación K(t) y(t). La ecuación diferencial resultante tiene la misma forma:
pero ahora ya no se trata de un sistema invariante en el tiempo (en caso que se tome 
para que sea posible estudiar la invariancia temporal).
para que sea posible estudiar la invariancia temporal).Ahora ¡ojo!, ya que K(t) podría ser una respuesta a impulso con la cual hay que convolucionar y(t) para obtener la salida del bloque K(t); esa sería otra interpretación "natural" del bloque K(t) en un contexto restringido a sistemas lineales invariantes en el tiempo.
Al perder de vista el significado del diagrama de bloques, me confundí pensando en otra interpretación, nada "natural", que da lugar a un sistema completamente distinto:
donde para llegar a una ecuación diferencial hay que aplicar con cuidado el teorema de Leibniz que permite derivar bajo el signo de integración y que sinceramente no recordaba en el momento, nos queda como ejercicio :)
Les pido disculpas por mi confusión y espero que sirva para que recordemos prestar atención a cómo interpretamos un bloque que pretende representar un sistema: es decir, a cómo mapea el conjunto de entradas en el conjunto de salidas.