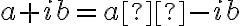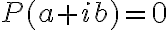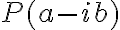Buenas, en esta parte del ejercicio se nos pide demostrar que, como a + ib es raiz de P(z), demostrar que a - ib también lo es.
Mi duda es, como sería el procedimiento correcto para demostrar dicha propiedad.
El razonamiento que yo sigo es el siguiente;
Si a + ib es raíz de P(z), entonces P(a +ib) = 0, y si a - ib también es raíz, P(a - ib) = 0 por lo que P(a + ib) = P(a - ib) = 0
así que a + ib = a - ib lo que deja como resultado 2ib = 0, lo que (según yo entiendo) deja como resultado que esta propiedad se cumple si y solo si b = 0.
Y, a mi parecer, ese resultado no es del todo correcto, agradecería una ayuda con este ejercicio.
Saludos, Francisco.