Hola,
En el 3.2.b logré obtener el resultado de z pero no logro entender cómo interpretar esa información geométricamente.
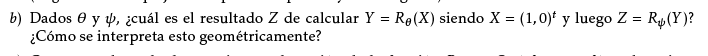
Tendría X = (1,0)t , Y = (Cos θ, Sin θ)t , Z = (Cos Ψ x Cos θ - Sin Ψ x Sin θ , Sin Ψ x Cos θ + Cos Ψ x Sin θ)t
¿Cómo interpreto eso geométricamente?
Gracias de antemano!
Hola Joaquín,
Capaz que la interpretación geométrica es más fácil verla solo para el vector Y, la cual es tomar el vector (1,0) y rotarlo θ (si esto no lo llegas a visulizar, probá hacer un dibujito). Aplicando el mismo razonamiento, el vector Z es tomar el vector Y y rotarlo Ψ, o lo que es lo mismo tomar el vector (1,0) y rotarlo θ+Ψ. Esto último se conecta con la pregunta siguiente de relacionar el valor de Z con unas "famosas fórmulas trigonométricas".
Hacete algunos dibujos para ver si lo visualizas bien, y si seguís sin verlo preguntá de nuevo.
Saludos
Si pudieran aclararme esto, lo agradecería :)
Si suponiendo un valor determinado de \(\theta\) te ayuda a visualizarlo mejor, hacelo sin problemas, pero también lo podes hacer de forma genérica para un \(\theta\) y un \( \psi \) cualquiera.
Hola, Bruno
No estoy entendiendo muy bien como encarar este ejercicio. Ya vi las otras preguntas que respondieron pero no entiendo muy bien. Yo ya tengo lo que es Y pero no entiendo como encontrar Z. Y si una vez que tenga Z, debo otorgarle un valor a \( \Theta y \psi \) para calcular que pasa cuando los sumo?
Gracias por la ayuda!
Hola Gabriela,
Para hallar $$Z$$ tenés que hacer el mismo procedimiento que hiciste para hallar $$Y$$, solo que en vez de hacer $$G_\theta (1,0)^t$$ vas a hacer $$G_\psi Y$$.
Luego, la idea no es darle ningún valor particular ni a $$\theta$$ ni a $$\psi$$, sino que es algo cualitativo. O sea, aplicar $$G_\theta$$ a $$(1,0)^t$$ es rotar $$\theta$$ grados al vector $$(1,0)^t$$ obteniendo $$Y$$, y después para hallar $$Z$$ agarrás $$Y$$ y lo rotas $$\psi$$ grados más, esto es equivalente a agarrar al vector $$(1,0)^t$$ y rotarlo $$\theta+\psi$$ grados (esta es otra manera de obtener a $$Z$$, y de la igualad de estas dos expresiones obtenés las "famosas fórmulas trigonométricas").
Cualquier cosa preguntá de nuevo.
Saludos