Hola,
En el ejercicio 3.1.c nos dicen que tenemos que calcular la inversa de S pero no entiendo a qué le debo hacer la inversa o cómo escribir el resultado final.
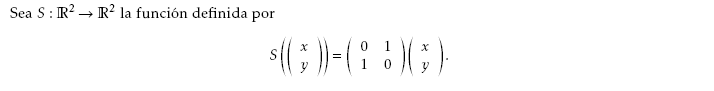
Si multiplico las dos matrices de S no podría hacer la inversa ya que no daría una matriz cuadrada, entonces solo le podría hacer la inversa a la primera matriz que sí es cuadrada. ¿Cómo escribo el resultado final? ¿Escribo la matriz inversa y le pongo multiplicando al lado la otra matriz con incógnitas?
Gracias de antemano!
según como yo lo hice, solamente hallas la inversa de la matriz cuadrada compuesta por unos y ceros. Ya qué la matriz columna que se encuentra la derecha, sólo está ahí para señalar cuáles son las incógnitas
Buenas,
Efectivamente, como dice Andrea, la matriz S es simplemente la matriz de 2x2 compuesta por unos y ceros. Se presenta multiplicada por el vector (x y)' debido a que lo que se presenta es una función, no únicamente una matriz.
En la parte (c), aparte de probar que la función es biyectiva, la matriz a partir de la cual se debe calcular su inversa es
$$ S = \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right)$$
Saludos