CDIVV-2S: Ejercicio 5

Hola, quería consultar por las partes b, c y d del ejercicio 5. ¿Podrían darme una guía o pista para comenzar? Siento si es una molestia. Muchas graciaas.

Re: Ejercicio 5

de Silvina Jaquelin Ferreira Pereira - miércoles, 26 de agosto de 2020, 04:29

Hola como estas, esos tres los resolves con lo dado en el video tres desde el inicio hasta el minuto 44.

Habla sobre raíces de los complejos, de ahí podrás resolverlos.

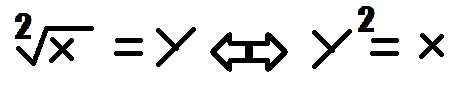
Observa por ejemplo que la raiz cuadrada de un numero, es otro numero que multiplicado por si mismo, me da el numero de dentro de la raíz, lo que puse en la foto. (disculpa que se vea tan mal)

Ya sabemos que en el caso de los reales son dos, valores, uno negativo y otro positivo. Obvie eso en la explicación.

Ahora imagina que esos X he Y que puse ahi, no son reales, y son complejos.

En el caso de los complejos hallar la raíz no es como en los reales, por ende utilizamos la segunda parte de mi fotito abajo.

Como no conoces la raíz de X complejo, sabes que tiene que existir al menos un complejo Y tal que elevado al numerito de la raíz, te de X. Te creas un Y genérico, lo elevas al numerito que corresponda y luego igualas Y elevado a X. Luego sacas los valores de modulo y de ángulos correspondientes para que ambos sean iguales. (trabajando siempre en notación polar)

SI TE ENTREVERE O NO SE ENTIENDE DIME, PUEDO INTENTAR EXPLICARLO MEJOR.

DE LO CONTRARIO, MIRATE EL LA PARTE DE VIDEO QUE TE SUGERI.

Re: Ejercicio 5

de Veronica Rumbo - miércoles, 26 de agosto de 2020, 09:38

Hola Joaquina, primero que nada, ninguna molestia ¡Para eso es el foro!

Como complemento a lo que dice Silvina, tené en cuenta que la definición tiene implicancias a nivel del módulo y el ángulo del complejo en cuestión:

$|\sqrt[n]{z}| = \sqrt[n]{|z|}$ (la raíz del módulo es el módulo de la raiz)

$n Arg(\sqrt[n]{z}) = Arg(z) +2k\pi$ (el ángulo de la raíz enésima mulitplicado por n, da el ángulo original, módulo $2\pi$ ).

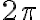Fijate, en particular, qué implicancias tiene esto para las raíces de la unidad.

Si con estas ayudas ves que sigue sin salir, no dudes en escribir y la seguimos. Saludos.