Nos piden probar que el P(de los z conjugados) es igual al conjugado de P(z). Al tener como dato que los coeficientes del polinomio son reales, concluí que P(z)=conjugado de P(z) pero el problema es en como llegar a que eso es igual a P(z conjugado). Tengo la idea de tener que trabajar un poco con raíces genéricas complejas, pero no logro entender como. Si me pueden guiar un poco se agradece, muchas gracias!!
Hola Iván. Tené cuidado que hay una afirmación que no es cierta: 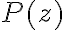 no tiene por que coincidir con
no tiene por que coincidir con 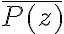 . Por ejemplo supongamos que el polinomio es
. Por ejemplo supongamos que el polinomio es 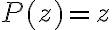 . Tomando
. Tomando 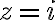 tengo que
tengo que  y
y 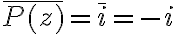 . No son iguales.
. No son iguales.
Volviendo a la igualdad original, que queremos probar, no hay necesidad de pensar en raíces genéricas. La idea es usar las distintas propiedades de la conjugación. Te recomiendo considerar un polinómio genérico 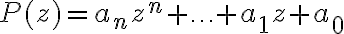 y usar las propiedades de la conjugación para hallar
y usar las propiedades de la conjugación para hallar 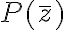 y
y 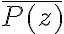 .
.
Espero te sirva de guía. Saludos.
(Editado por Carolina Puppo - envío original miércoles, 19 de agosto de 2020, 15:38)
Entendí. Ahí salió, muchisimas gracias!!
Tengo una consulta con esto:
Me da la impresión que para lograr verificar la parte a) hay un paso que no me queda claro. En el conjugado del polinomio usamos la propiedad de la suma de conjugados para separar el polinomio en sumandos de conjugados. El tema es que ahí pasamos de tener conjugadoDe(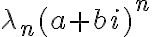 ) a
) a 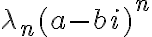 . Ese paso es válido? Porque me parecería que no es tan directo el paso siendo que tenemos una potencia en el medio.
. Ese paso es válido? Porque me parecería que no es tan directo el paso siendo que tenemos una potencia en el medio.
Gracias!
Me da la impresión que para lograr verificar la parte a) hay un paso que no me queda claro. En el conjugado del polinomio usamos la propiedad de la suma de conjugados para separar el polinomio en sumandos de conjugados. El tema es que ahí pasamos de tener conjugadoDe(
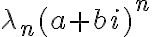 ) a
) a 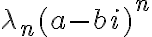 . Ese paso es válido? Porque me parecería que no es tan directo el paso siendo que tenemos una potencia en el medio.
. Ese paso es válido? Porque me parecería que no es tan directo el paso siendo que tenemos una potencia en el medio.Gracias!

