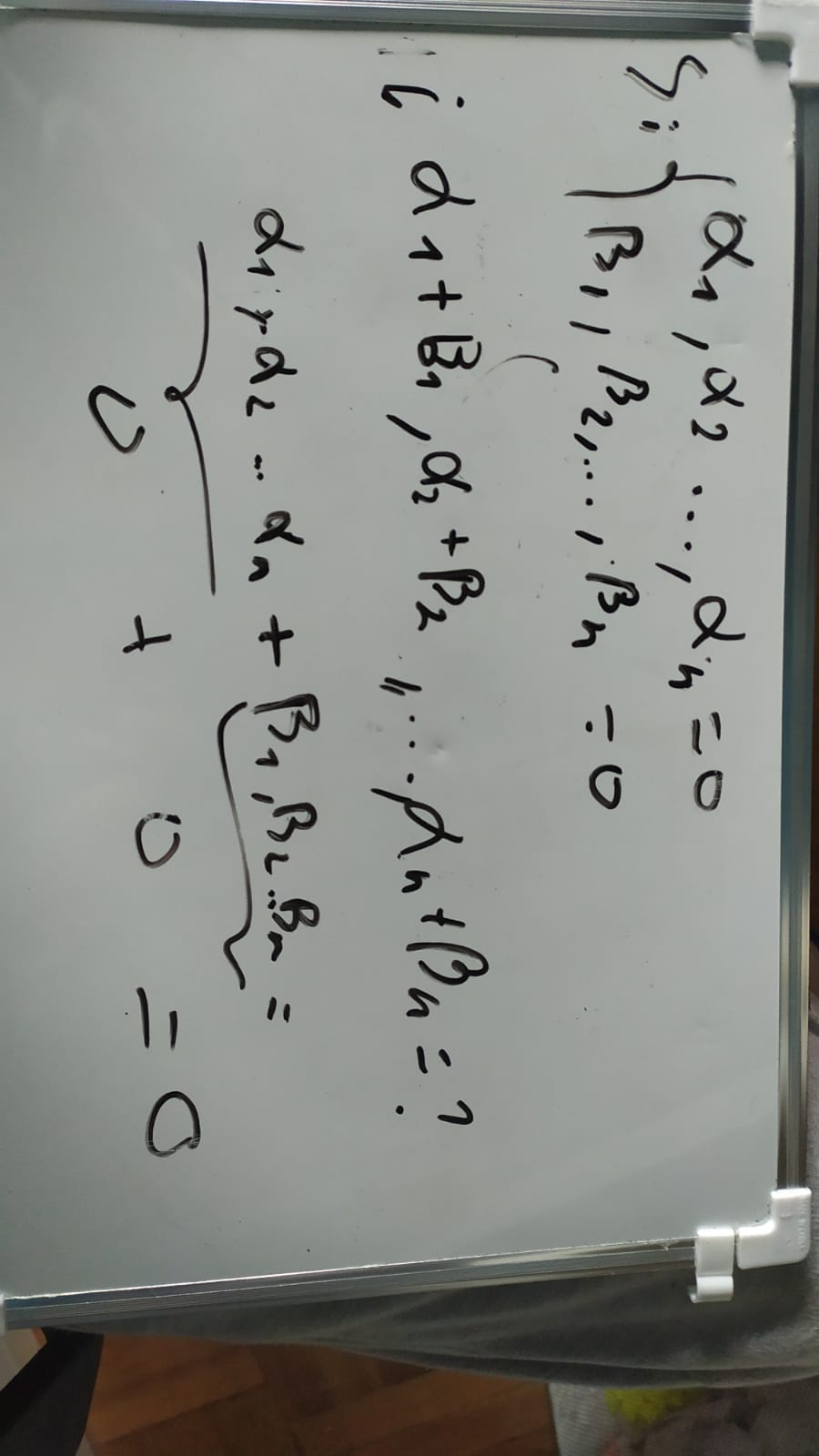Hola Nataly,
Copio partes de tu redacción y hago comentarios:
"Sea (α₁,α₂...αₙ)∈ Sol (S) y sea (cα₁,cα₂...cαₙ)∈ Sol (S´)".
Se pide probar que: SI (α₁,α₂...αₙ)∈ Sol (S) ENTONCES (cα₁,cα₂...cαₙ)∈ Sol (S). Como es para un MISMO sistema, no hay ningún S', es siempre S.
La forma "SI bla, bla, bla, ENTONCES patatín, patatán" se llama IMPLICACIÓN. Tienes que SUPONER "bla, bla, bla" y DEMOSTRAR "patatín, patatán". A "bla, bla, bla" le llamamos hipótesis y a "patatín, patatán" la tesis.
No tiene sentido entonces que digas "y sea (cα₁,cα₂...cαₙ)∈ Sol (S)", ya que es eso justamente lo que tienes que demostrar. Decir "sea" significa suponer que eso ya es cierto. Si tienes que probar algo, no puedes suponerlo.
"Por
transformación elemental, donde sea multiplicar un número c≠0 tal que
cFᵢ, puesto que (α₁,α₂...αₙ) satisface toda ecuación de S, entonces
satisface a todo Fᵢ del sistema lineal. Y por esa misma propiedad,
también lo hace (cα₁,cα₂...cαₙ)."
Esta frase es tremendamente confusa. No estoy seguro de entender qué quisiste decir. Lo ideal en una prueba es escribir frases cortas y bien precisas. Normalmente una prueba tiene el aspecto de una receta, donde uno toma las hipótesis (en este caso, (α₁,α₂...αₙ)∈ Sol (S)) y les hace cosas para probar la tesis (en este caso (cα₁,cα₂...cαₙ)∈ Sol (S)).
Un buen comienzo puede ser este: Sea (α₁,α₂...αₙ)∈ Sol (S) y sea Fi de la forma ai1x1+ ... + aim xm= 0 la i-ésima ecuación del sistema. Como (α₁,α₂...αₙ)∈ Sol (S)), entonces ai1 α1+ ... + aim αm= 0.... ahora lo que te falta es convencerte de que (cα₁,cα₂...cαₙ) también satisface la ecuación Fi. Luego, como el razonamiento vale para cualquiera de las ecuaciones Fi, entonces (cα₁,cα₂...cαₙ)∈ Sol (S). Fíjate además que nadie dice que c≠0 sea una hipótesis.
La misma estructura de razonamiento la vas a aplicar para probar que la suma de soluciones es solución. De hecho nadie te pide probar que el sistema sea indeterminado, sino que te dicen que pruebes que si tienes dos soluciones, sumándolas obtienes una solución. Esas dos soluciones podrían incluso ser la misma, no importa. Además lo que argumentaste de hecho es falso: los sistemas homogéneos pueden ser determinados.
Tarea: Repasar en la primera clase de teórico de OpenFing la definición de sistema lineal y de conjunto solución (ver el teórico a partir del minuto 10:00).
Consejo general: Lo primero a lo que hay que atinar frente a un ejercicio es a escribir lo que significa cada concepto definido que estás usando. ¿Qué forma general tiene un sistema lineal homogéneo? ¿Qué significa ser solución de ese sistema?
Haré una afirmación radical y, por lo tanto, exagerada: las definiciones en matemática son las cosas más importantes que existen y SIEMPRE hay que estar seguro de conocer las definiciones antes de hacer cualquier otra cosa. Uno no pierde el tiempo repasando definiciones.
Cordiales saludos.