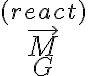Foro de consultas generales

Estimado Rodrigo,

vamos a considerar la reducción con respecto a 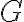$G$ del sistema de reactivas (estamos viendo el efecto neto de las articulaciones en $A$ y $B$) que actúa sobre el rígido:

(i) tenemos una reacción resultante

(ii) tenemos un momento dado $\vec M_G^{(react)}$

y veamos qué podemos sacar a partir de las cardinales:

(I) Como el centro de masas está sobre el eje de giro, su aceleración es cero; por lo tanto, si planteamos la primera cardinal, resulta que la reacción resultante debe compensar al peso: esta parte es claramente independiente del tiempo

(II) Al plantear la segunda cardinal desde 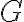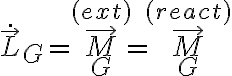$G$: $\dot {\vec L}_G=\vec M_G^{(ext)}=\vec M_G^{(react)}$ y derivar el momento angular, nos encontramos con que el momento de las reactivas es o bien nulo (si se cumple la condición que tenemos que hallar) o bien un vector que rota con el rígido y por lo tanto es variable en el tiempo. Este último caso es el que se correspondería con tener reacciones en $A$ y $B$ variables en el tiempo. Hasta acá contestás la pregunta correctamente, si vamos un poco más en detalle:

la suma de las reacciones en cada articulación debe respetar que compensa al peso, pero dando en conjunto un momento reactivo no nulo (sólo es no nulo bajo la condición pedida). Podés pensar para esto en que cada reacción en $A$ o $B$ es la suma de dos vectores: uno constante que soporta el peso y uno rotatorio: la suma de las partes estáticas compensa al peso, la parte rotatoria debe ser opuesta entre la de $A$ y  la de $B$ de forma que se anulen entre sí en la suma y por lo tanto sean un par, cuyo momento también es rotatorio.

Saludos,

Ariel.