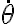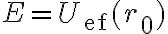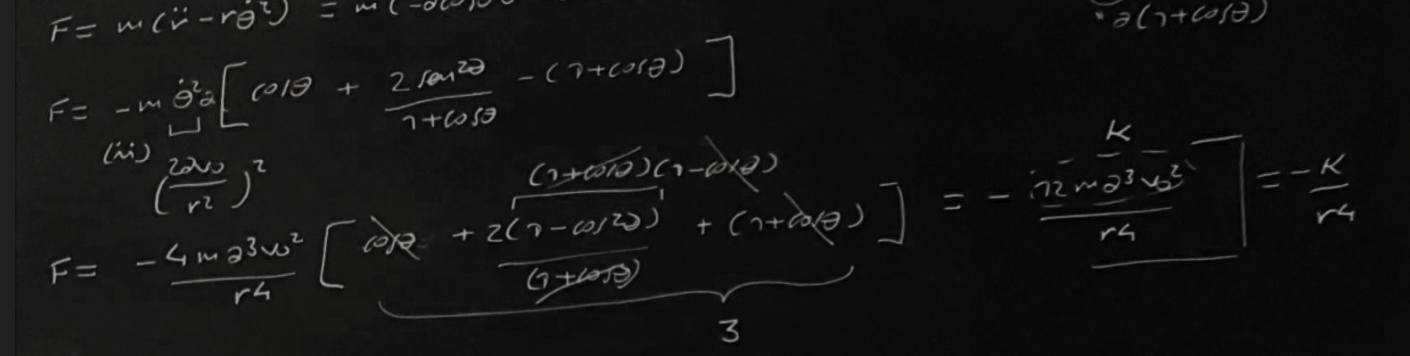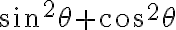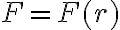hola, gracias por la pronta respuesta.
Perdón por el error de theta punto. Ahi me di cuenta del error q estaba teniendo. La verdad este tipo de cosas me parece que estan de sobra en los ejercicios, en este caso al menos a mi me ocurrió que tuve todo el procedimiento bien, pero por simplemente hacer un cambio matemático que ni siquiera estaba sugerido se pierden los puntos. Y la verdad es que un cambio matemático de este estilo no aporta para nada, quita tiempo en saber la expresión, y no suma al evaluar si el estudiante sabe o no mecánica.. No se evalua nada con eso. Me refiero al de escribir 1-cos^2, como 1 binomio. Recuerden que la matemática con la que ustedes los físicos se manejan, no es la misma que la nuestra.. me refiero a en lo que nosotros hacemos hincapié, a diferencia de ustedes. Queda como crítica constructiva sin ánimo de ofender a nadie para próximas evaluaciones.
No es nada en contra tuyo Nicolás, es en contra de esta metodología (y no me refiero a la múltiple opción), cosas como estas son las que al estudiante le hace perder tiempo innecesario, incluso siendo de desarrollo los cálculos no quedarían nada cómodos para seguir con las otras partes, sino nos dábamos cuenta de esa equivalencia matemática. Fíjense que incluso, de antemano me tenia que dar cuenta de sacar el factor común theta punto, cuando en teoría uno siempre tiende a escribir todo sin ninguna dependencia para llegar al resultado que se pedía.
Saludos, y espero que al menos lo reflexionen..