Foro de consultas generales

Hola,

Me da la impresi'on que est'as pensando en el momento del sistema de cuatro barras con respecto a un eje perpendicular al plano de las cuatro barras y en ese caso una solucion del estilo de lo que planteas es correcta.

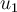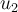Sin embargo, el ejercicio pide el momento con respecto al eje $u_{1}$ (o $u_{2}$, el momento con respecto a cualquiera de estos ejes es identico por simetr'ia). Ah'i la situaci'on es distinta.

Pensemos en el momento con respecto a 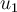$u_{1}$. En este caso tenemos dos barras que son paralelas al eje y dos barras perpendiculares al eje. Entonces el momento total va a ser 2x(momento de una barra paralela) + 2x(momento de una barra perpendicular).

El momento de una barra con respecto a un eje paralelo a la barra que pasa por su centro de masa es cero. Cuando corremos el eje manteniendolo paralelo a una distancia a/2 usamos steinter y la contrib al momento es

I_paralelo = M(a/2)^2

El momento de una barra con respecto a un eje perpendicular a ella por su centro es Ma^2/12. Cuando lo trasladamos del cm al centro del sistema de cuatro barras el eje se mueve en una direccion paralela al propio eje, entonces la contribucion del termino de steiner es cero. La contribucion al momento por el centro del cuadrilatero de una sola de las barras perpendiculares a 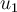 $u_{1}$ es entonces

I_perp = Ma^2/12

Como tenemos dos barras paralelas a 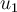 $u_{1}$ y dos perpendiculares el resultado es

I = 2 I_paralelo + 2 I_perp

que es el resultado que da la solucion

espero que esto responda tu pregunta

de otro modo no dudes en repreguntar

saludos

guzman