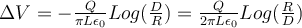Examen Febrero 2020

Examen Febrero 2020

de Francisco Santini Caballero -
Número de respuestas: 11

Hola!

En el ejercicio 1c, nos piden calcular la diferencia de potencial eléctrico entre los ejes de los cilindros.

En la solución dice que es lo mismo que calcular la diferencia entre los bordes de los cilindros, porque dentro de ellos no hay campo eléctrico.

Pero creo que está mal, porque hay campo eléctrico dentro de un cilindro producido por el otro cilindro. ¿Es asi?

Dejo el link de la solución

 https://eva.fing.edu.uy/pluginfile.php/8744/mod_page/content/91/Sol_Feb_2020.pdf?time=1581969789063


Saludos

En respuesta a Francisco Santini Caballero

Re: Examen Febrero 2020

de Ignacio Grosso San Roman -

Cuando calcula el potencial separa en dos integrales, una para campo. Cada integran tiene como intervalos desde el bode del cilindro que produce el campo hasta el eje del otro, asi abarca de eje a eje.

La integral para el campo 1 va de X=R (borde del primer cilindro) hasta X=D (eje del segundo cilindro) y para el campo 2 va de X=0 (eje del primer cilindro) hasta X=D-R (borde del segundo cilindro).

Lo que si me pasa es que a mi la solucion de la integral, el logaritmo me queda ln(R/D) en vez de ln(D/R) como en la solucion.

En respuesta a Ignacio Grosso San Roman

Re: Examen Febrero 2020

de Juan Andres Muniz -

Buenas, lo que dicen ustedes está bien. En la solución hay un signo de menos que desaparece en la última línea. De esa forma 

\Delta V = -\frac{Q}{\pi L \epsilon_0} Log(\frac{D}{R}) = \frac{Q}{2 \pi L \epsilon_0} Log(\frac{R}{D})

Una forma de darse cuenta qué tiene sentido es notar que la diferencia de potencial desde el cilindro de la derecha hasta el de la izquierda (Q a -Q) debe ser negativa. La solución da un resultado positivo porque D es mayor que R.

Cualquier cosa a las órdenes.
En respuesta a Juan Andres Muniz

Re: Examen Febrero 2020

de Ignacio Grosso San Roman -
Otra cosa que no entiendo es por que en el ejercicio 2b, cuando toma la parte real de la correinte, utiliza seno en vez de coseno.

Si no me equivoco, la parte real de un complejo expresado en exponencial es la parte del coseno, ya que Me^{i \alpha} = M(\cos(\alpha)+i\sin(\alpha)) siendo coseno la parte real y seno la parte imaginaria.
En respuesta a Ignacio Grosso San Roman

Re: Examen Febrero 2020

de Florencia Benitez Martinez -

Hola Ignacio,

Si, tal vez no es la mejor forma de escribirlo, pero tené en cuenta que se refiere a lo siguiente:

Por más que los voltajes y las intensidades las representamos como exponenciales complejas, lo que medimos son cantidades reales.

Un complejo es, como bien decís, z=a+ib, donde a y b son reales. 

Por lo tanto, dependiendo de la función trigonométrica de la que estemos hablando, la parte del complejo que tomamos para la cantidad en cuestión.

En este caso, el potencial es V=Vo sen(wt), lo que corresponde a la proyección del complejo en el eje vertical, o sea, el número real b.

No es que tome la parte real en sí, sino que proyecta y obtiene una cantidad real.

Saludos.

En respuesta a Florencia Benitez Martinez

Re: Examen Febrero 2020

de Ignacio Grosso San Roman -

Muchas gracias, ya comprendi.

Resulta tambien que tenia escritas con coseno las formulas en mi cuaderno de teorico, pero luego volviendo a ver otros ejercicios y ejemplos que tenia, efectivamente es seno la funcion que se usa, de ahi gran parte de mi confusion.

En respuesta a Ignacio Grosso San Roman

Re: Examen Febrero 2020

de Florencia Benitez Martinez -

Ignacio,

cuidado que lo que tenés en tu cuaderno de teórico no está mal. Se pueden usar ambas.

De hecho, recordá que cos(wt - pi/2) = sen(wt), por lo tanto, ambas funciones sólo difieren en las condiciones iniciales.

Saludos!

En respuesta a Florencia Benitez Martinez

Re: Examen Febrero 2020

de Ignacio Grosso San Roman -

Entonces lo importante seria ver la funcion del potencial (en este caso V(t)=V0sen(wt) ) y saber que la corriente va a tener la misma funcion pero con el angulo desfasado por la impedancia?