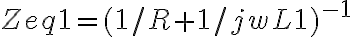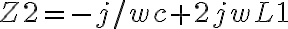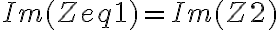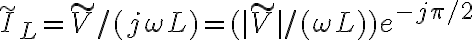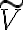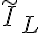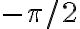Primero, tu dibujo al principio de la página 2 es incorrecto ya que la fase de la corriente por el inductor es 90 grados menor que la fase del voltaje. La forma de darte cuenta es dibujar las dos corriente y determinar el fasor asociado a la corriente por la fuente. El fasor asociado a la corriente por el resistor está bien.
A muy groso modo, físicamente, el inductor tiende a oponerse al pasaje de corriente (ley de Lenz). Por eso retrasa respecto al voltaje sobre el inductor. En un capacitor, la corriente es máxima cuando se comienza a cargar (Q es proporcional a V), por lo que la corriente por capacitor adelanta al voltaje en el capacitor.
Para el caso de un inductor, la corriente que pasa por él es
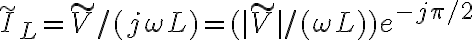 ,
,
donde el fasor 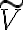 es el asociado al voltaje de la fuente, que asumí tiene fase 0 (es real). La fase del fasor corriente por el inductor
es el asociado al voltaje de la fuente, que asumí tiene fase 0 (es real). La fase del fasor corriente por el inductor 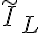 es
es 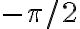 , es decir -90 grados, respecto a la fase del voltaje. Fijate que es una igualdad entre números complejos, así que fases y módulos tiene que ser iguales a ambos lado.
, es decir -90 grados, respecto a la fase del voltaje. Fijate que es una igualdad entre números complejos, así que fases y módulos tiene que ser iguales a ambos lado.
De esta forma, el fasor de la corriente total debe tener fase negativa y atrasa con respecto al voltaje.
Si esto te quedó claro, tratá de dibujar los fasores asociados con las corrientes por el capacitor y el segundo inductor y pensar que debe cumplirse para que el factor de potencia se 1. Creo que la idea que tenés está ahí, a menos de estos signos, pero gráficamente es bastante más sencillo.
Si tenés dudas, volvé a preguntar sin problema. No es sencillo. En todo caso, te recomiendo mires el material que colgamos, hay tres videos y unas notas, y se discuten estos casos.
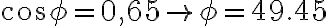 , la tangente de este es igual a L1/R , obtengo L1
, la tangente de este es igual a L1/R , obtengo L1