Hola.
La regla de introducción del existe dice:
![\infer[I\exists]{\hline(\exists x )\varphi}{ D \\ ...\\ \varphi[t/x]} \infer[I\exists]{\hline(\exists x )\varphi}{ D \\ ...\\ \varphi[t/x]}](https://eva.fing.edu.uy/filter/tex/pix.php/6f1a217e3200cf11218fbe3e9b12015f.gif)
Recordemos que no importa cómo se construya la derivación, una vez terminada, siempre se lee desde las hojas hasta la raíz (de arriba hacia abajo).
Entonces el punto es que la regla, no hace una sustitución, sino que cuando se avanza hacia la conclusión se deshace una sustitución.
De esta forma,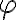 que está al lado del existe, es cualquier fórmula tal que si sustituimos x por t, nos de la fórmula de arriba de la regla. Esto hace que yo pueda (des)sustituir lo que me conviene.
que está al lado del existe, es cualquier fórmula tal que si sustituimos x por t, nos de la fórmula de arriba de la regla. Esto hace que yo pueda (des)sustituir lo que me conviene.
Esto hace que:
![\infer[I\exists] {\hline (\exists z)\, f(x) =' z}{f(x) =' f(x)} \infer[I\exists] {\hline (\exists z)\, f(x) =' z}{f(x) =' f(x)}](https://eva.fing.edu.uy/filter/tex/pix.php/d37f4a4189fecb682d12c5f2272dcca6.gif) Es correcta porque
Es correcta porque ![(f(x) =' z)[f(x)/z] = (f(x)='f(x)) (f(x) =' z)[f(x)/z] = (f(x)='f(x))](https://eva.fing.edu.uy/filter/tex/pix.php/748445495e9802f6c90869ce7b541b7c.gif) .
.
![\infer[I\exists] {\hline (\exists z)\, z =' f(x)}{f(x) =' f(x)} \infer[I\exists] {\hline (\exists z)\, z =' f(x)}{f(x) =' f(x)}](https://eva.fing.edu.uy/filter/tex/pix.php/c1fafdb2765a700c1a0204b642c6529e.gif) Es correcta porque
Es correcta porque ![(z=' f(x))[f(x)/z] = (f(x)='f(x)) (z=' f(x))[f(x)/z] = (f(x)='f(x))](https://eva.fing.edu.uy/filter/tex/pix.php/3c5af017f96fdff03a56f399bff61493.gif) .
.
![\infer[I\exists] {\hline (\exists z)\, z =' f(x)}{f(x) =' f(x)} \infer[I\exists] {\hline (\exists z)\, z =' f(x)}{f(x) =' f(x)}](https://eva.fing.edu.uy/filter/tex/pix.php/c1fafdb2765a700c1a0204b642c6529e.gif) Es correcta porque
Es correcta porque ![(z=' z)[f(x)/z] = (f(x)='f(x)) (z=' z)[f(x)/z] = (f(x)='f(x))](https://eva.fing.edu.uy/filter/tex/pix.php/be7a837d17f0309afa87346b10044a3e.gif) .
.
Espero que quede claro. Si no, pregunten de nuevo !!!!
Saludos
La regla de introducción del existe dice:
![\infer[I\exists]{\hline(\exists x )\varphi}{ D \\ ...\\ \varphi[t/x]} \infer[I\exists]{\hline(\exists x )\varphi}{ D \\ ...\\ \varphi[t/x]}](https://eva.fing.edu.uy/filter/tex/pix.php/6f1a217e3200cf11218fbe3e9b12015f.gif)
Recordemos que no importa cómo se construya la derivación, una vez terminada, siempre se lee desde las hojas hasta la raíz (de arriba hacia abajo).
Entonces el punto es que la regla, no hace una sustitución, sino que cuando se avanza hacia la conclusión se deshace una sustitución.
De esta forma,
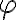 que está al lado del existe, es cualquier fórmula tal que si sustituimos x por t, nos de la fórmula de arriba de la regla. Esto hace que yo pueda (des)sustituir lo que me conviene.
que está al lado del existe, es cualquier fórmula tal que si sustituimos x por t, nos de la fórmula de arriba de la regla. Esto hace que yo pueda (des)sustituir lo que me conviene.Esto hace que:
![\infer[I\exists] {\hline (\exists z)\, f(x) =' z}{f(x) =' f(x)} \infer[I\exists] {\hline (\exists z)\, f(x) =' z}{f(x) =' f(x)}](https://eva.fing.edu.uy/filter/tex/pix.php/d37f4a4189fecb682d12c5f2272dcca6.gif) Es correcta porque
Es correcta porque ![(f(x) =' z)[f(x)/z] = (f(x)='f(x)) (f(x) =' z)[f(x)/z] = (f(x)='f(x))](https://eva.fing.edu.uy/filter/tex/pix.php/748445495e9802f6c90869ce7b541b7c.gif) .
. ![\infer[I\exists] {\hline (\exists z)\, z =' f(x)}{f(x) =' f(x)} \infer[I\exists] {\hline (\exists z)\, z =' f(x)}{f(x) =' f(x)}](https://eva.fing.edu.uy/filter/tex/pix.php/c1fafdb2765a700c1a0204b642c6529e.gif) Es correcta porque
Es correcta porque ![(z=' f(x))[f(x)/z] = (f(x)='f(x)) (z=' f(x))[f(x)/z] = (f(x)='f(x))](https://eva.fing.edu.uy/filter/tex/pix.php/3c5af017f96fdff03a56f399bff61493.gif) .
.![\infer[I\exists] {\hline (\exists z)\, z =' f(x)}{f(x) =' f(x)} \infer[I\exists] {\hline (\exists z)\, z =' f(x)}{f(x) =' f(x)}](https://eva.fing.edu.uy/filter/tex/pix.php/c1fafdb2765a700c1a0204b642c6529e.gif) Es correcta porque
Es correcta porque ![(z=' z)[f(x)/z] = (f(x)='f(x)) (z=' z)[f(x)/z] = (f(x)='f(x))](https://eva.fing.edu.uy/filter/tex/pix.php/be7a837d17f0309afa87346b10044a3e.gif) .
.Espero que quede claro. Si no, pregunten de nuevo !!!!
Saludos
