En la clase 19 - Deducción de Predicados 2 (Año 2019)
En el minuto 30 se inicia a derivar (Para todo x)(Existe y) f(x)=´y terminando en el minuto 37
No entiendo el paso de introducción del existe, porque puedo hacer la sustitución en un solo f(x)? no debería sustituir en los dos?.
En el minuto 36 el profesor comenta exactamente lo que yo no entiendo ¨A uno le parece que tendría que haber cambiado todos los f(x), y no, yo elijo cual cambio¨
Porque puedo elegir cual cambiar?
Esto creo que es lo mismo que se explica en la clase 18 desde el minuto 34:30 hasta el minuto 40
Pero tampoco entiendo porque de x=´x puedo derivar (Existe x)x=´y
![\infer[I\exists]{\hline(\exists x )\varphi}{ D \\ ...\\ \varphi[t/x]} \infer[I\exists]{\hline(\exists x )\varphi}{ D \\ ...\\ \varphi[t/x]}](https://eva.fing.edu.uy/filter/tex/pix.php/6f1a217e3200cf11218fbe3e9b12015f.png)
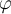
![\infer[I\exists] {\hline (\exists z)\, f(x) =' z}{f(x) =' f(x)} \infer[I\exists] {\hline (\exists z)\, f(x) =' z}{f(x) =' f(x)}](https://eva.fing.edu.uy/filter/tex/pix.php/d37f4a4189fecb682d12c5f2272dcca6.png)
![(f(x) =' z)[f(x)/z] = (f(x)='f(x)) (f(x) =' z)[f(x)/z] = (f(x)='f(x))](https://eva.fing.edu.uy/filter/tex/pix.php/748445495e9802f6c90869ce7b541b7c.png)
![\infer[I\exists] {\hline (\exists z)\, z =' f(x)}{f(x) =' f(x)} \infer[I\exists] {\hline (\exists z)\, z =' f(x)}{f(x) =' f(x)}](https://eva.fing.edu.uy/filter/tex/pix.php/c1fafdb2765a700c1a0204b642c6529e.png)
![(z=' f(x))[f(x)/z] = (f(x)='f(x)) (z=' f(x))[f(x)/z] = (f(x)='f(x))](https://eva.fing.edu.uy/filter/tex/pix.php/3c5af017f96fdff03a56f399bff61493.png)
![(z=' z)[f(x)/z] = (f(x)='f(x)) (z=' z)[f(x)/z] = (f(x)='f(x))](https://eva.fing.edu.uy/filter/tex/pix.php/be7a837d17f0309afa87346b10044a3e.png)