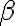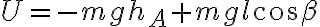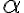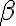Buenas,
Tengo una duda sobre el ejercicio 4. En el trato de establecer la primera y segunda cardinal para la condición de equilibrio tomando la normal en A como un vector horizontal y un momento MA . Llego a expresiones con senos y cosenos de los ángulos alpha y beta pero no logro sacar ninguna condición de los mismo. Agradezco cualquier guía o ayuda.
El ejercicio se puede hacer por energía: hallando los extremos relativos de la energía potencial para ver cuáles posiciones son de equilibrio, y luego hallando los mínimos para ver cuáles de esas posiciones de equilibrio son estables.
En tu procedimiento observo que agregas un momento en A para la normal. Pero ese momento es cero, ya que la normal está aplicada en el punto de apoyo.
Buenas, estoy teniendo el mismo problema que Julian, pude plantear las ecuaciones cardinales para la barra, pero no logro encontrar una relación entre los angulos para que se cumpla el equilibrio. Me gustaría alguna guía sobre como seguir, muchas gracias desde ya
Hola Valentín,
antes que nada, más allá de hacerlo planteando cardinales a la barra, no estaría mal seguir la recomendación de Ricardo en cuanto a a hacer un planteo por energía y verificar que se llega a lo mismo.
En cualquier caso, van a necesitar una relación entre 
y 
que sale del Teorema del Seno, ya que los lados opuestos a cada uno de estos ángulos del triángulo son conocidos.
Les dejo por ahí la sugerencia, sigan con el ejercicio y cualquier otra duda pregunten nomás.
Saludos,
Ariel.
Hola,
Al hacerlo por energia tenes que considerar todas las posiciones que puede tener la barra para las cuales la cuerda se mantiene tensa y el extremo de la barra que no sta atado a la cuerda se mantiene en contacto con la pared. Es decir, tenes que pensar como si la cuerda fuera una barra rigida sin masa y consideras el potencial de todo ese sistema.
Con estas consideraciones, resulta que el punto A es movil: si la cuerda se mantiene tensa y cambia el angulo alfa, para que la barra se mantenga apoyada, necesariamente tiene que cambiar el angulo beta y al mismo tiempo moverse el punto A.
Dado que el punto A se mueve, no tiene sentido tomarlo como cero del potencial. Ahi esta tu error.
Lo mejor es tomar como referencia del potencial el punto en que la cuerda se une a la pared. Entonces el potencial lo podes escribir
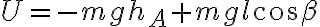
siendo 
la distancia entre el punto donde la cuerda se une a la pared y el punto A. Esta distancia la podes hallar facilmente en terminos de 
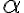y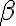 
. Despues, tenes que hallar una relacion entre estos dos angulos que te permita expresar uno en terminos del otro, dado que estan vinculados como mencione antes, si cambia 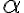, tiene que cambiar 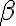de manera acord para que la cuerda se mantenga rigida y la barra con un extremo en la pared.
Una vez que lograste expresar el potencial en terminos de un unico angulo, hallando los extremos del potencial se encuentran los puntos de equlibrio
Trate de explicarte el problema pero dejando para que vos rellenes algunos de los agujeros que faltan. Si tenes alguna duda o esto no responde tu duda no dudes en repreguntar.
Saludos
G