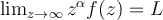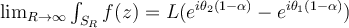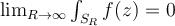No me doy cuenta como sale ésta demostración.
Si uno descompone esa integral como:
la curva gamma una semicircunferencia en semiplano inferior de radio R.
La integral en el arco de cfa. es lo que habria que acotar y hacer tender R a infinito y verificar que es cero (es lo que no me sale por deformación de curvas)
Quizás por la desigualdad de Cauchy podes acotarlo y verlo. pero no me salió.
se agradece alguna idea,
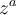
![\int_{[-R,R]} f(t)dt + \int_{S_R} f(z)dz = \int_{\gamma R} f(z)dz \int_{[-R,R]} f(t)dt + \int_{S_R} f(z)dz = \int_{\gamma R} f(z)dz](https://eva.fing.edu.uy/filter/tex/pix.php/7214caed15c129017f2a52a032cef15f.png)