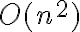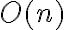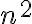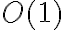Prog2: Complejidad del filtrado en un arbol binario.

Buenas, me surgio la siguiente duda analizando la complejidad de filtrar un arbol binario segun una cota en su dato, como en el ejercicio 4 del practico 4. Lo que pense fue lo siguiente (siguiendo la solucion que dieron del ejercicio) :

El peor caso se da cuando la raiz no pasa el filtro y ambos subarboles son no vacios, pues se debe buscar el elemento mayor del subarbol izquierdo. A su vez, la busqueda es O(n). Entonces si tengo un arbol donde en todos los nodos se produce el peor caso, tendria una cota O(n^2), porque para cada nodo tengo que hacer cosas de O(n) y tengo n nodos.

Es correcto el razonamiento? Se puede hacer en menor tiempo?

Re: Complejidad del filtrado en un arbol binario.

de Fernando Fernandez - sábado, 9 de mayo de 2020, 09:44

El razonamiento es correcto y efectivamente 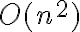$O(n^2)$ es una cota del tiempo de ejecución. Pero hay que recordar que O es el análogo a "menor o igual". O sea que en principio 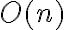$O(n)$ también podría ser una cota superior.

Mirá el ejemplo de la slide 22 del teórico. Hay una iteración de hasta n pasos y en su cuerpo hay también una posible iteración de n pasos. Podemos pensar que en el peor caso habrá 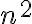$n^2$ pasos, como consecuencia de tener que hacer las n iteraciones del ciclo exterior y en cada una de ellas tener que hacer la iteración interna. Y por lo tanto 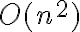$O(n^2)$ sería una cota superior pero 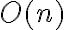$O(n)$ no. Pero un análisis más fino nos muestra que esto último no es cierto y que en realidad 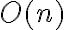$O(n)$ es una cota. ¿Te das cuenta por qué?

El pero caso en el ciclo interno solo puede darse una vez y además hace que termine el ciclo externo.

En el ejercicio que vos planteás si se diera el caso que mencionás las búsquedas no serían 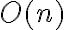$O(n)$ , sino 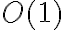$O(1)$ porque el resultado del subárbol izquierdo sería vacío (hay que recordar que la búsqueda del mayor no se hace en el subárbol original sino en el resultado de la llamada recursiva).

Vamos al otro extremo. ¿Cuándo la búsqueda es más costosa? Cuando la raíz no cumple la condición, el subárbol derecho consiste en un único nodo que la cumple y el subárbol izquierdo es una cadena de n - 2 nodos que cumplen la condición y que tienen solo hijos derechos, excepto el último que es una hoja. Esa búsqueda requiere n-2 pasos, por lo que es 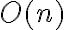$O(n)$ pero no 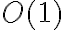$O(1)$ . Pero si se dio ese caso como cada nodo cumple la condición su procesamiento fue 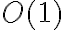$O(1)$ (no hubo búsquedas). El procesamiento de todos los nodos es 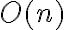$O(n)$ y por regla de la suma el costo de todo el algoritmo es $O(n)$ .

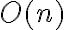Podemos ir un paso más. Supongamos que en el subárbol izquierdo pase algo similar al principal. Es decir en la raíz del árbol principal no se cumple la condición y su subárbol derecho tiene un único nodo que la cumple. En el subárbol izquierdo la raíz tampoco cumple la condición, su subárbol derecho también tiene un único nodo, llamémosle ID, que cumple la condición, y los n-4 nodos de su subárbol izquierdo cumplen la condición y forman una cadena hacia la derecha. La búsqueda para el subárbol izquierdo va a tener n - 4 pasos. Pero ahora la búsqueda para el árbol raíz va a tener solo 2 pasos, porque el subárbol izquierdo tiene un subárbol derecho con un solo nodo, ID.

Y así podríamos seguir. Lo que ocurre, en este ejercicio, es que un paso muy costoso hace que sean poco costosos los siguientes.

Debe quedar claro que en este curso no vamos a pedir análisis como este.