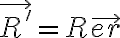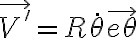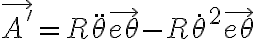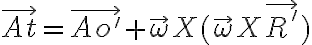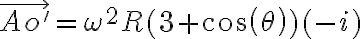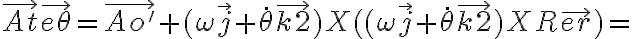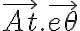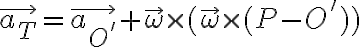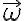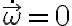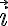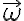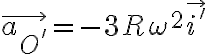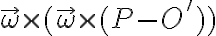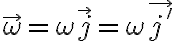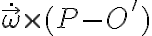MecNew: Ejercicio 1 parcial mayo 2008

Buenas ! , Al aplicar el teorema de coriolis entre:

S1:{O,i,j,k1} (rojo en la imagen) un sistema fijo centrado en el eje de giro .

S2:{O´,i',j',k2}(azul en la imagen) que gira con la guía circular

nos surgieron algunas dudas.

En el S2 tenemos las magnitudes R , V , A de la masa m como :

$\vec{R'}=R \vec{er}$

$\vec{V'}=R \dot{ \theta } \vec{e \theta }$

$\vec{A'}=R \ddot{ \theta } \vec{e \theta } -R \dot{ \theta }^2 \vec{e \theta }$

Entonces $\vec{At} = \vec{Ao'}+ \vec{ \omega }X( \vec{ \omega }X \vec{R'} )$

Si utilizo R' como lo plantee anteriormente , no llego a la misma aceleración de transporte (solo quiero su componente en e tita) que plantea la solución

ya que $\vec{Ao'}= \omega ^2R(3+cos( \theta ))(-i)$

Entonces

$\vec{At} \vec{e \theta } = \vec{Ao'} +(\omega \vec{j} + \dot{ \theta } \vec{k2})X((\omega \vec{j} + \dot{ \theta } \vec{k2})XR \vec{er}) =$

al calcular esto , algunos terminos quedan en direcciones perpendiculares a e tita , por lo que no afectan a $\vec{At}. \vec{e \theta }$ .

Pero al descomponer lo que queda según i no me queda lo mismo q la solucion

donde $\vec{At}. \vec{e \theta }$ representa la aceleración de transporte según e phi

213 palabras

Re: Ejercicio 1 parcial mayo 2008

de Ricardo Marotti - domingo, 3 de mayo de 2020, 15:11

En tu desarrollo tenés algunos errores. Empecemos con lo que está bien. Están bien las expresiones de la aceleración relativa y la expresión general de la aceleración de arrastre:

$\vec{a_T} = \vec{a_{O'}} + \vec{ \omega } \times ( \vec{ \omega } \times (P-O') )$

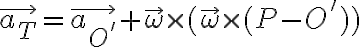
porque 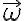$\vec{ \omega }$ es constante, entonces 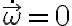$\dot{ \vec{ \omega } } = 0$ . Observá que la velocidad angular que va aquí es la del sistema S' en torno a un sistema fijo.

Ahora no estoy seguro que los versores del sistema rojo tuyo sean constantes, por lo que ese sistema no es un sistema absoluto (fijo). O sea, como dibujaste tu sistema 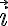$\vec{i}$ giraría con velocidad angular 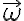$\vec{ \omega }$ , entonces no es fijo.

Pero en este ejercicio no se tiene por qué dibujar el sistema fijo. Usaremos solo el sistema móvil que dibujaste.

La aceleración de O' no es la que vos escribiste. Es solo:

$\vec{a_{O'}} = - 3R \omega^2 \vec{i'}$

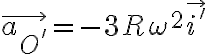
porque O' hace un movimiento circular uniforme de velocidad angular ω y radio 3R en torno al eje fijo.

Para calcular el otro término 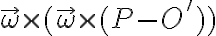$\vec{ \omega } \times ( \vec{ \omega } \times (P - O') )$ , la velocidad angular que hay que usar es solamente:

$\vec{ \omega } = \omega \vec{j} = \omega \vec{j'}$

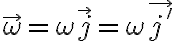
(que es la que es constante para que no agreguemos el término 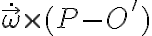$\dot{ \vec{ \omega } } \times (P-O')$ ) porque no es la velocidad angular de la partícula, sino que es la velocidad angular del sistema móvil respecto al sistema fijo, que solo tiene un giro simple de velocidad angular ω en torno al eje de giro. O sea, en tu desarrollo está mal adicionar el término en 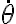$\dot{ \theta }$ a la velocidad angular. La velocidad angular $\dot{ \theta }$ está vinculada al movimiento relativo. No al movimiento de arrastre.

Y eso te debería dar el resultado de la solución del parcial.

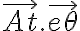301 palabras