En efecto, hay una hipótesis implícita que es que las transformadas F(jw) y G(jw) existen.
La función 1/t tiene área infinita cuando t va a cero, y el seno que tiende a cero como t lo compensa.
La exponencial compleja que aparece en la transformada no aporta a regular el area de 1/t porque su límite en cero es uno.
Incluso la delta que generaliza las funciones puede verse como un pulso que crece a infinito, pero su área se mantiene acotada (igual a uno) por eso aceptamos que la integral exista y esté bien definida la transformada de Fourier. Esto no pasa con 1/t.
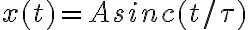y nos piden calcular su CTFT. Me surgen un par en la resolucion de esto. Por un lado, utilizando la propiedad de dualidad tenemos que 
y llegue a que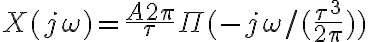 
que no estoy seguro si es correcto. Pero tambien lo intente pensar por el lado de que 
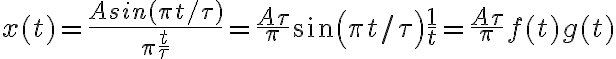con la idea de utilizar la propiedad del producto 
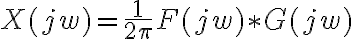. Pero g(t) no es absolutamente convergente, en consecuencia no existe la G(jw), ¿qué es lo que sucede en este caso? ¿Por qué funciona hallar la CTFT utilizando dualidad y no la propiedad de la multiplicación? Gracias, saludos.